Der Impuls als Bewegungsmenge: Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
(→‎Trägheitsgesetz (1. Newtonsches Axiom))
(→‎Beispiele)
 
(14 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt)
Zeile 7: Zeile 7:
 
  Bild:Golfball.jpg|Diese Bälle...
 
  Bild:Golfball.jpg|Diese Bälle...
 
  Bild:Tennisball.jpg|...können das auch.  
 
  Bild:Tennisball.jpg|...können das auch.  
−
  Bild:Curling_Abstoß.jpg|<ref>[http://commons.wikimedia.org/wiki/File:Martin_Sesaker_at_the_2012_Youth_Winter_Olympics.jpg Bild von Ralf Roletschek, CC by SA 3.0]</ref>Beim Curling  muss man dem Stein den richtigen Schwung mitgeben,
+
  Bild:Dosenwerfen_Impuls_Styroporball_2.jpg|Dosenwerfen!
−
  Bild:Curling_Besen.jpg|damit er genau am Ziel stehenbleibt.
+
  Bild:Kegel_Kugel.jpg|Kegeln!
−
Bild:Luftkissenpuck.jpg|Wie funktioniert dieser "Fußball"?
+
−
Bild:Einkaufswagen_voll.png| Wie bewegt sich ein "angeschubster" Einkaufswagen?
+
 
</gallery>
 
</gallery>
  
Zeile 19: Zeile 17:
 
Weitere Beispiele sind der Luftkissenpuck (Fußball), ein Mensch auf einem Bürodrehstuhl oder Experimente am Luftkissentisch oder -bahn.
 
Weitere Beispiele sind der Luftkissenpuck (Fußball), ein Mensch auf einem Bürodrehstuhl oder Experimente am Luftkissentisch oder -bahn.
  
−
====Das Wasserbehältermodell====
+
====Versuch: Dosenwerfen====
 +
[[Datei:Dosenwerfen_Impuls_Styroporball_2.jpg|thumb|upright|Am Boden liegt links der Knetball und rechts der Styroporball.]]
 +
;Aufbau
 +
Man versucht einen Stapel Dosen mit einem geworfenem Ball umzuschmeißen. Eine Person hat einen Styroporball, die andere einen Ball aus Knete.
 +
;Beobachtung
 +
Um mit dem Knetball die Dosen umzuwerfen, muß man nicht so fest werfen, es genügt zu treffen.
 +
<br>Nur ein ganz schneller Styroporball kann auch eine Dose umwerfen.
 +
;Folgerung
 +
Die Bälle brauchen eine gewisse Menge an "Wucht", um eine Dose umzuwerfen. Diese "Wucht" ist groß, wenn der Ball eine große Masse hat und eine große Geschwindigkeit hat.
 +
 
 +
==Definition des Impulses==
 +
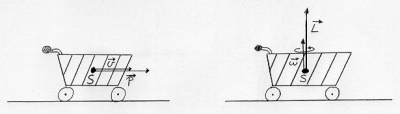
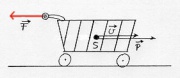
[[Image:Mechanik_Bewegungszustand.jpg|thumb|400px|Die Bewegungsmenge eines Einkaufswagens.]]
 +
* Ein Ball enthält viel "Bewegung", wenn er schnell ist und er eine große Masse hat. Die physikalische Größe, welche die Bewegungsmenge angibt, heißt "Impuls". <br>Man legt den Impuls daher als Produkt der beiden Größen fest: <math>p = m \, v</math> <br>Die Einheit des Impulses ist deshalb ein Kilogramm mal Meter pro Sekunde, oder kürzer ein "Huygens"<ref>Die Einheit ist nach [https://de.wikipedia.org/wiki/Christiaan_Huygens Christiaan Huygens] (1629–1695) benannt und wird auf Deutsch "Heugens" gesprochen.</ref>: <math>1 \,\rm Hy = 1\,\rm kg \cdot \rm \frac{m}{s}</math> <br>
 +
*Umgangssprachlich versteht man unter "Impuls" etwas anderes als in der Physik!
 +
**Eine Anregung, ein Anreiz, ein Ansporn: "Der Telefonanruf ihrer Freundin war der entscheidende Impuls doch noch für die Arbeit zu lernen." ; "Der Comic ist ein guter Impuls für eine Diskussion."
 +
**Etwas plötzliches, kurzzeitiges: "Manchmal handelt er sehr impulsiv ohne nachzudenken." 
 +
 
 +
:{|class="wikitable"
 +
|style="border-style: solid; border-width: 4px "|
 +
Impuls- und Geschwindigkeitsvektor sind parallel,
 +
<br>die Masse ist der Proportionalitätsfaktor:
 +
 
 +
:<math>\vec p = m \vec v</math>
 +
:<math>[\vec p\,] = \mathrm{1kg \frac{1m}{1s} = 1Hy}</math> (lies: Huygens)
 +
|}
 +
 
 +
==Das Wasserbehältermodell==
 
Mit Hilfe der Regler kann man die Masse und die Geschwindigkeit des Autos verändern. (Die Massen- und Geschwindigkeitsangaben sind in kg und in m/s und deshalb etwas ;) unrealistisch.)
 
Mit Hilfe der Regler kann man die Masse und die Geschwindigkeit des Autos verändern. (Die Massen- und Geschwindigkeitsangaben sind in kg und in m/s und deshalb etwas ;) unrealistisch.)
  
Zeile 25: Zeile 49:
  
 
{{#widget:Iframe  
 
{{#widget:Iframe  
−
|url=http://tube.geogebra.org/material/iframe/id/296557/width/1222/height/770/border/888888/rc/false/ai/false/sdz/true/smb/false/stb/false/stbh/true/ld/false/sri/true/at/preferhtml5
+
|url=https://www.geogebra.org/material/iframe/id/jGJRWYCw/width/1325/height/666/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/false/ctl/false
 
|width=1000
 
|width=1000
 
|height=500
 
|height=500
Zeile 36: Zeile 60:
 
|style="border-style: solid; border-width: 4px "|  
 
|style="border-style: solid; border-width: 4px "|  
 
Jeder Gegenstand behält ohne Wechselwirkung mit einem anderen Körper
 
Jeder Gegenstand behält ohne Wechselwirkung mit einem anderen Körper
−
<br> seinen Impuls <math>\vec p</math>  in Menge und Richtung.
+
<br> seinen Impuls <math>\vec p = m \, \vec v</math>  in Menge und Richtung.
 
|}
 
|}
  
Zeile 46: Zeile 70:
 
Drückt (zieht) man mit einer [[Die Kraft|Kraft]] <math>\vec F</math> an einem Gegenstand,  
 
Drückt (zieht) man mit einer [[Die Kraft|Kraft]] <math>\vec F</math> an einem Gegenstand,  
 
<br> so wird die Richtung oder die Menge des Impulses <math>\vec p</math> verändert.
 
<br> so wird die Richtung oder die Menge des Impulses <math>\vec p</math> verändert.
−
 
−
Dreht man mit einem Drehmoment <math>\vec M</math> ("Drehkraft") an einem Gegenstand,
 
−
<br> so wird die Richtung oder die Menge des Drehimpulses <math>\vec L</math> verändert.
 
 
|}
 
|}
  
−
==Aufgaben==
+
==[[Aufgaben zum Impuls als Bewegungsmenge|Aufgaben]]==
−
;1) Berechne jeweils die Impulsmenge
+
−
:a) Ein Vogel mit der Masse 100 g fliegt mit 36 km/h.
+
−
:b) Ein Fußgänger (m=72 kg) läuft mit 5 km/h.
+
−
:c) Ein Auto (m=1 t) fährt mit 36 km/h.
+
−
 
+
−
;2) Anke und ihr Papa fahren zusammen Rad.
+
−
:Anke wiegt 40 kg, ihr Vater 90 kg, jedes ihrer Räder 10kg. Sie fahren mit 18 km/h nebeneinander.
+
−
:a) Wieviel Impuls steckt in Anna, in ihrem Vater und wieviel in den beiden Rädern?
+
−
:Stelle dies mit dem Wasserbehältermodell dar.
+
−
:b) Wie schnell muss Anke fahren, um genausoviel Impuls wie ihr Vater zu haben? (mit Rädern)
+
−
:Stelle auch dies im Wasserbehältermodell dar.
+
−
 
+
−
;3) Ball und Gewehrkugel
+
−
:Ein Tennisball (m=57g) kann bei einer Geschwindigkeit von 5 km/h einen Holzklotz umschmeißen.
+
−
:Wie schnell muß dazu eine Luftgewehrkugel sein, wenn sie nur 0,541 g Masse hat?
+
−
 
+
−
===[[Aufgaben zum Impuls als Bewegungsmenge - Lösungen|Lösungen]]===
+
  
 
==Links==
 
==Links==
−
*[https://www.univie.ac.at/physikwiki/index.php/LV001:LV-Uebersicht/Videos/Rollende_Zylinder Video] von herabrollender Dose und Zylinder. (Fakultät für Physik Uni Wien; eLearning) Probleme mit Flash-Player
 
−
*[https://www.youtube.com/watch?v=BYM_ZjDYhL4 Video] von herabrollenden Zylindern mit unterschiedlicher Messeverteilung. (youtube: "Versuch auf schiefer Ebene - Versuch" von "Noob Physik")
 
−
*[http://www.youtube.com/watch?v=4OD4aDlAiZI Video] der Drehschwingung eines Menschen auf einem Drehstuhl. (youtube: "Trägheitsmomente" von "Wissenschaftskanal1")
 
  
 
==Fußnoten==
 
==Fußnoten==
 
<references />
 
<references />

Aktuelle Version vom 13. Mai 2019, 16:44 Uhr

(Physik Sekundarstufe I > Kraft und Bewegung ("Dynamik"))

Beispiele

  • Eine Luftgewehrkugel

  • kann dieses Brettchen umstoßen!

  • Diese Bälle...

  • ...können das auch.

  • Dosenwerfen!

  • Kegeln!

  • Verschiedene Bälle, am besten gleich groß aber mit unterschiedlichen Massen, fangen und werfen. (Oder "Kegeln", denn dabei spielt die Gewichtskraft keine Rolle. Oder "Dosenwerfen" mit verschiedenen Bällen.)
  • Ein sich schnell drehendes Fahrrad-Rad kann man nicht so ohne weiteres anschubsen, abbremsen oder kippen. Es "wehrt sich".
  • Beispiel mit reibungsarmen Einkaufswagen: Der Wagen bewegt sich geradlinig und behält seine Geschwindigkeit bei. Auch die Drehung des Wagen ändert sich nicht.

Weitere Beispiele sind der Luftkissenpuck (Fußball), ein Mensch auf einem Bürodrehstuhl oder Experimente am Luftkissentisch oder -bahn.

Versuch: Dosenwerfen

Am Boden liegt links der Knetball und rechts der Styroporball.
Aufbau

Man versucht einen Stapel Dosen mit einem geworfenem Ball umzuschmeißen. Eine Person hat einen Styroporball, die andere einen Ball aus Knete.

Beobachtung

Um mit dem Knetball die Dosen umzuwerfen, muß man nicht so fest werfen, es genügt zu treffen.
Nur ein ganz schneller Styroporball kann auch eine Dose umwerfen.

Folgerung

Die Bälle brauchen eine gewisse Menge an "Wucht", um eine Dose umzuwerfen. Diese "Wucht" ist groß, wenn der Ball eine große Masse hat und eine große Geschwindigkeit hat.

Definition des Impulses

Die Bewegungsmenge eines Einkaufswagens.
  • Ein Ball enthält viel "Bewegung", wenn er schnell ist und er eine große Masse hat. Die physikalische Größe, welche die Bewegungsmenge angibt, heißt "Impuls".
    Man legt den Impuls daher als Produkt der beiden Größen fest: [math]p = m \, v[/math]
    Die Einheit des Impulses ist deshalb ein Kilogramm mal Meter pro Sekunde, oder kürzer ein "Huygens"[1]: [math]1 \,\rm Hy = 1\,\rm kg \cdot \rm \frac{m}{s}[/math]
  • Umgangssprachlich versteht man unter "Impuls" etwas anderes als in der Physik!
    • Eine Anregung, ein Anreiz, ein Ansporn: "Der Telefonanruf ihrer Freundin war der entscheidende Impuls doch noch für die Arbeit zu lernen." ; "Der Comic ist ein guter Impuls für eine Diskussion."
    • Etwas plötzliches, kurzzeitiges: "Manchmal handelt er sehr impulsiv ohne nachzudenken."

Impuls- und Geschwindigkeitsvektor sind parallel,
die Masse ist der Proportionalitätsfaktor:

[math]\vec p = m \vec v[/math]
[math][\vec p\,] = \mathrm{1kg \frac{1m}{1s} = 1Hy}[/math] (lies: Huygens)

Das Wasserbehältermodell

Mit Hilfe der Regler kann man die Masse und die Geschwindigkeit des Autos verändern. (Die Massen- und Geschwindigkeitsangaben sind in kg und in m/s und deshalb etwas ;) unrealistisch.)

  • Mit welcher Masse und welcher Geschwindigkeit enthält das Auto einen Impuls von 10 Hy?

Trägheitsgesetz (1. Newtonsches Axiom)

Mit Hilfe des Impulses kann man das Trägheitsgesetz genauer fassen:

Jeder Gegenstand behält ohne Wechselwirkung mit einem anderen Körper
seinen Impuls [math]\vec p = m \, \vec v[/math] in Menge und Richtung.

Veränderungsgesetz (2. Newtonsches Axiom)

Eine Veränderung der Bewegungsmenge durch eine Kraft. Der Impuls des Wagens nimmt ab.

Drückt (zieht) man mit einer Kraft [math]\vec F[/math] an einem Gegenstand,
so wird die Richtung oder die Menge des Impulses [math]\vec p[/math] verändert.

Aufgaben

Links

Fußnoten

  1. ↑ Die Einheit ist nach Christiaan Huygens (1629–1695) benannt und wird auf Deutsch "Heugens" gesprochen.
Von „http://www.schulphysikwiki.de/index.php?title=Der_Impuls_als_Bewegungsmenge&oldid=15296“