Überlagerung von harmonischen Schwingungen (Fouriersyntese): Unterschied zwischen den Versionen
K (→Frequenzanalyse mit dem Computer) |
(→Versuch: Messung von Luftschwingungen) |
||
| Zeile 26: | Zeile 26: | ||
Die beiden Schwingungen überlagern sich zu einer Schwingung, deren Amplitude sich ändert. | Die beiden Schwingungen überlagern sich zu einer Schwingung, deren Amplitude sich ändert. | ||
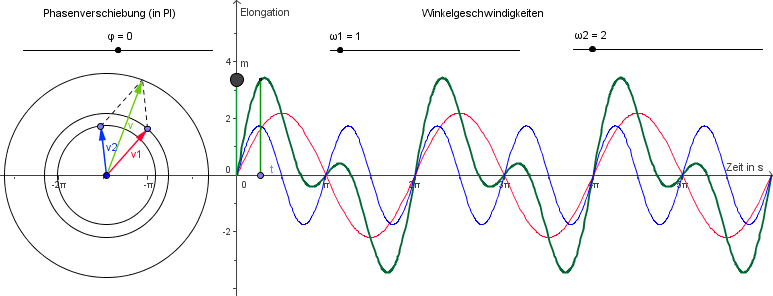
| − | Im Zeigerdiagramm rotieren zwei Zeiger mit leicht unterschiedlicher Winkelgeschwindigkeit. | + | Im Zeigerdiagramm rotieren zwei Zeiger mit leicht unterschiedlicher Winkelgeschwindigkeit. |
| − | Hat sich der Phasenunterschied auf <math>\pi</math> vergrößert, so sind die Schwingungen gegenphasig und die Amplitude wird klein oder sogar Null. Sind die Schwingungen wieder in Phase und die Zeiger parallel, so wird die Amplitude maximal. | + | Hat sich der Phasenunterschied auf <math>\pi</math> vergrößert, so sind die Schwingungen gegenphasig und die Amplitude wird klein oder sogar Null. Sind die Schwingungen wieder in Phase und die Zeiger parallel, so wird die Amplitude maximal. |
| + | |||
| + | Die Summe der Zeiger ist nicht immer exakt in der Mitte der beiden anderen, weshalb seine Winkelgeschwindigkeit nicht konstant ist. Die Überlagerung ist also keine harmonische Schwingung mehr. | ||
[[Bild:Schwingung_Überlagerung_Schwebung_gleiche_Amplitude.png|none]] | [[Bild:Schwingung_Überlagerung_Schwebung_gleiche_Amplitude.png|none]] | ||
| Zeile 38: | Zeile 40: | ||
Für die Frequenz der Schwebung gilt: <math>f_s = |f_2-f_1|</math> | Für die Frequenz der Schwebung gilt: <math>f_s = |f_2-f_1|</math> | ||
| − | Das kann man folgendermaßen begründen: Es dauert t Sekunden, bis der schnellere Zeiger, den langsamen wieder eingeholt hat: | + | Das kann man folgendermaßen begründen: In der Zeit t drehen sich die Zeiger um die Winkel <math>\omega_1 \,t</math>, bzw um <math>\omega_2 \, t</math>. Es dauert t Sekunden, bis der schnellere Zeiger, den langsamen wieder eingeholt hat: |
| − | :<math>2 \pi = \omega_2 \, -\omega_1 \, t</math> | + | :<math>2 \pi = \omega_2 \, t - \omega_1 \, t</math> |
:<math>\Rightarrow t= \frac{\omega_2 - \omega_1}{2 \pi}</math> | :<math>\Rightarrow t= \frac{\omega_2 - \omega_1}{2 \pi}</math> | ||
| Zeile 45: | Zeile 47: | ||
:<math>\Rightarrow f_s= \frac{2 \pi}{\omega_2 - \omega_1} = f_2 - f_1</math> | :<math>\Rightarrow f_s= \frac{2 \pi}{\omega_2 - \omega_1} = f_2 - f_1</math> | ||
| − | Für die Frequenz der Überlagerung gilt: <math>f | + | Für die Frequenz der Überlagerung gilt: <math>f \approx \frac{f_1 + f_2}{2}</math> |
| − | + | ||
| + | Da die Überlagerung keine harmonische Schwingung ist, ist diese Angabe streng genommen nicht korrekt, denn die Winkelgeschwindigkeit und somit die Frequenz ist nicht konstant. Im zeitlichen Mittel ist aber der Summenzeiger der beiden Schwingungen ungefähr in der Mitte der beiden Zeiger, woraus sich als mittlere Frequenz der Mittelwert der überlagerten Schwingen ergibt. | ||
==Überlagerung von Schwingungen mit gleicher Frequenz== | ==Überlagerung von Schwingungen mit gleicher Frequenz== | ||
Version vom 2. Dezember 2006, 19:41 Uhr
Inhaltsverzeichnis
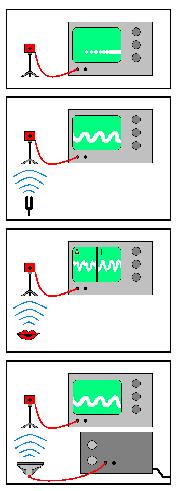
Versuch: Messung von Luftschwingungen
Aufbau:
Um Aussagen über die Überlagerung und Zerlegung von Schwingungen zu machen, haben wir zunächst einige Versuche durchgeführt. Dazu wurde ein Mikrofon an ein Oszilloskop angeschlossen, der die entsprechende graphische Darstellung der Schwingungen liefert. Das Mikrophon übersetzt die Druckveränderungen in Spannungsveränderungen, welche am Oszilloskop angezeigt werden. Die x-Achse der Darstellung ist die Zeit, die y-Achse die Spannung.
- Wir haben Töne erzeugt, wie z.B. gesungene Vokale oder eine Stimmgabel angeschlagen.
- Wir haben mit Hilfe eines Sinusgenerators, der an einen Lautsprecher angeschlossen ist und einer Stimmgabel gleichzeitig einen hohen und einen tiefen Ton erzeugt.
- Wir haben zwei Stimmgabeln gleichzeitig angeschlagen, wobei an einer ein Reiter befestigt war.
Beobachtung:
- Beim Singen von Vokalen z.B. konnte man feststellen, dass jeder Vokal eine charakteristische Kurve hat. Je reiner der Ton ist, desto deutlicher kann man eine Sinuskurve erkennen.
- Die angezeigte Kurve sieht aus, wie eine Überlagerung beider Töne.
- Bei den zwei Stimmgabeln hörte man einen wabernden Ton. (Waa-Waa-Waa) Dabei konnte man folgende Beobachtung machen: wenn der Frequenzunterschied der Stimmgabeln gering ist, ist die Frequenz kleiner. Ist aber der Frequenzunterschied groß, so ist die Frequenz größer. Auf dem Monitor wird eine Schwingung mit sich regelmäßig ändernden Amplituden angezeigt.
Erklärung
1.
2. Die Überlagerung ergibt sich im Zeigerdiagramm aus einem schnell drehenden und einem langsam drehenden Zeiger.
3. Mit Hilfe eines Reiters auf der Stimmgabel kann man die Frequenz verkleinern. Stellt man sich die Stimmgabel vereinfacht als Federpendel vor, so ist klar, dass die Vergrößerung der Masse eine geringe Frequenz zur Folge hat.
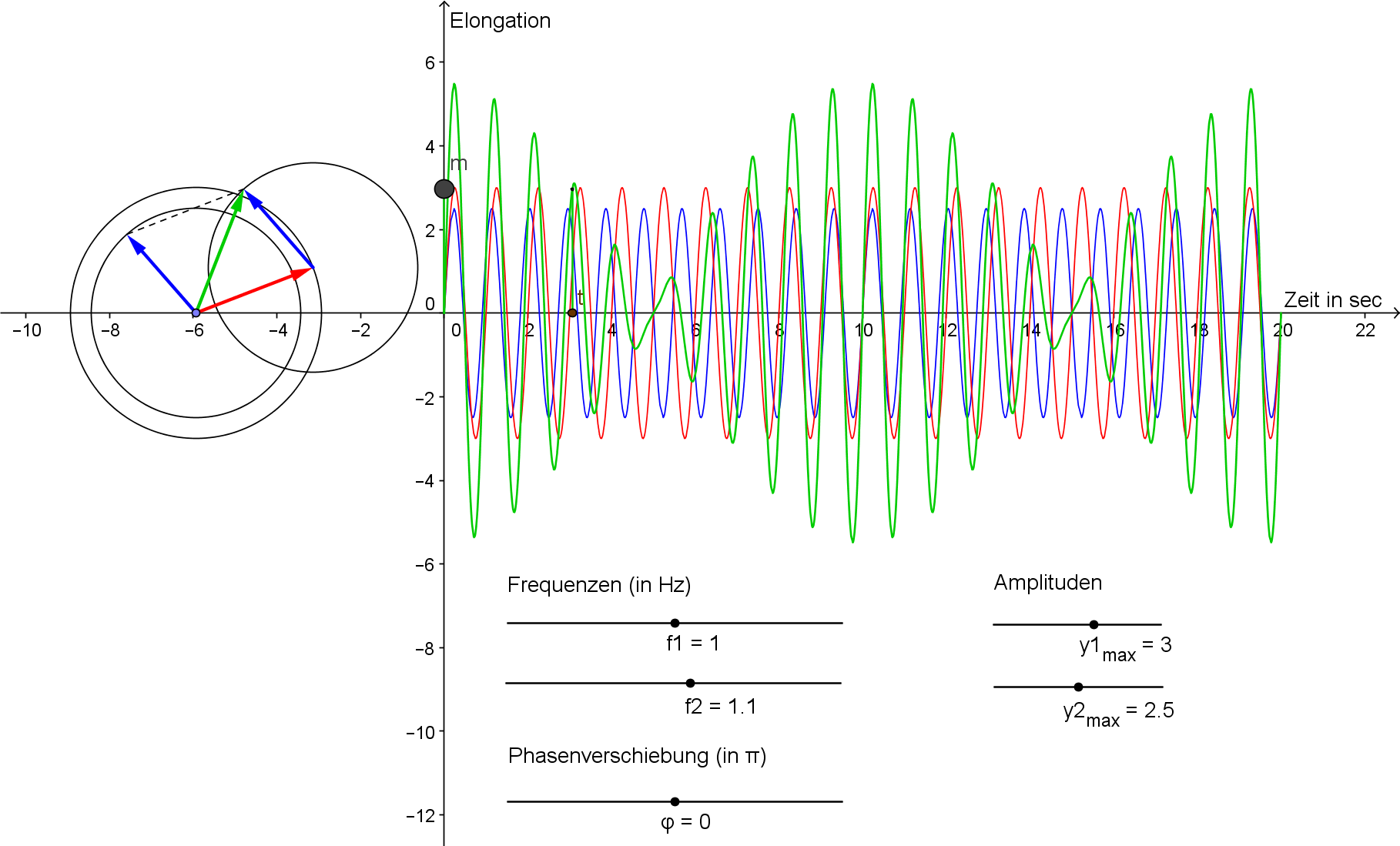
Die beiden Schwingungen überlagern sich zu einer Schwingung, deren Amplitude sich ändert. Im Zeigerdiagramm rotieren zwei Zeiger mit leicht unterschiedlicher Winkelgeschwindigkeit. Hat sich der Phasenunterschied auf [math]\pi[/math] vergrößert, so sind die Schwingungen gegenphasig und die Amplitude wird klein oder sogar Null. Sind die Schwingungen wieder in Phase und die Zeiger parallel, so wird die Amplitude maximal.
Die Summe der Zeiger ist nicht immer exakt in der Mitte der beiden anderen, weshalb seine Winkelgeschwindigkeit nicht konstant ist. Die Überlagerung ist also keine harmonische Schwingung mehr.
Diese Schwebung ist nicht so ausgeprägt, weil die Amplituden unterschiedlich sind:
Für die Frequenz der Schwebung gilt: [math]f_s = |f_2-f_1|[/math]
Das kann man folgendermaßen begründen: In der Zeit t drehen sich die Zeiger um die Winkel [math]\omega_1 \,t[/math], bzw um [math]\omega_2 \, t[/math]. Es dauert t Sekunden, bis der schnellere Zeiger, den langsamen wieder eingeholt hat:
- [math]2 \pi = \omega_2 \, t - \omega_1 \, t[/math]
- [math]\Rightarrow t= \frac{\omega_2 - \omega_1}{2 \pi}[/math]
- [math]\Rightarrow f_s= \frac{2 \pi}{\omega_2 - \omega_1} = f_2 - f_1[/math]
Für die Frequenz der Überlagerung gilt: [math]f \approx \frac{f_1 + f_2}{2}[/math]
Da die Überlagerung keine harmonische Schwingung ist, ist diese Angabe streng genommen nicht korrekt, denn die Winkelgeschwindigkeit und somit die Frequenz ist nicht konstant. Im zeitlichen Mittel ist aber der Summenzeiger der beiden Schwingungen ungefähr in der Mitte der beiden Zeiger, woraus sich als mittlere Frequenz der Mittelwert der überlagerten Schwingen ergibt.
Überlagerung von Schwingungen mit gleicher Frequenz
Alle nachfolgenden Simulationen sind mit einem Applet zur Überlagerung zweier harmonischer Wellen entstanden. (ca. 1MB)
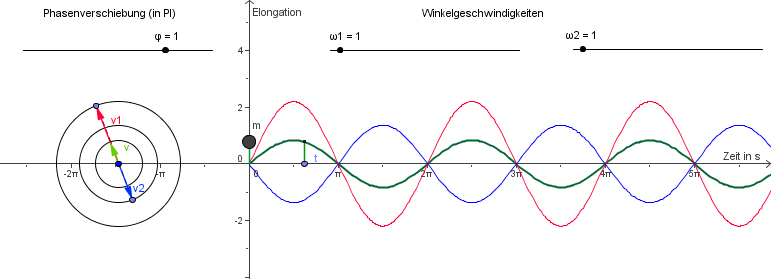
Überlagerung zweier Schwingungen mit gleicher Frequenz, ohne Phasenverschiebung mit unterschiedlicher Amplitude. Die Elongationen verstärken sich. Im Zeigerdiagramm addieren sich die Zeiger zu einem Zeiger mit größerer Länge. Alle Zeiger drehen sich gleichschnell.
Überlagerung zweier Schwingungen mit gleicher Frequenz, gegenphasig mit unterschiedlicher Amplitude. Die Elongationen schwächen sich. Im Zeigerdiagramm addieren sich die Zeiger zu einem Zeiger mit kleinerer Länge. Alle Zeiger drehen sich gleichschnell.
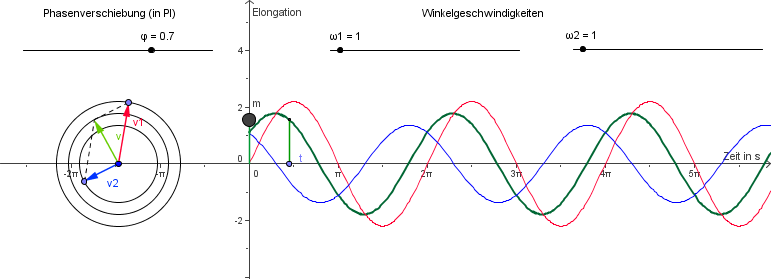
Überlagerung zweier Schwingungen mit gleicher Frequenz und mit Phasenverschiebung. Wiederum addieren sich die Zeiger, diesmal mit Hilfe eines Vektorparallelogramms. Auch hier drehen sich alle Zeiger gleichschnell.
Überlagern sich zwei harmonische Schwingungen, so entsteht eine harmonische Schwingung derselben Frequenz. Die Amplitude erhält man durch Zeigeraddition, sie hängt auch von der Phasenverschiebung ab.
Überlagerung von Schwingungen mit unterschiedlicher Frequenz
Überlagerung zweier Schwingungen mit dem Frequenzverhältnis von 1:2, ohne Phasenverschiebung mit unterschiedlicher Amplitude.
Bei der Überlagerung von harmonischen Schwingungen unterschiedlicher Frequenz entstehen im Allgemeinen keine harmonischen Schwingungen.
Versuch: Frequenzanalyse mit dem Computer
Aufbau:
Ein Mikrophon wird an einen Computer angeschlossen. (CASSY) Die Software analysiert die aufgenommene (nichtharmonische!) Schwingung, indem sie harmonische Schwingungen sucht, zu denen man die aufgenommene Schwingen überlagern kann. Das Programm muss also zu jeder Frequenz eine Amplitude suchen.
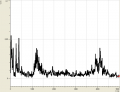
Angezeigt wird die Amplitude über der Frequenz, das sogenannte Frequenzspektrum oder auch Spektrum.
Wir singen verschiedene Töne und spielen Musikinstrumente.
Beobachtung:
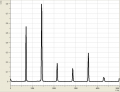
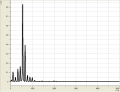
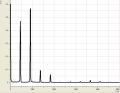
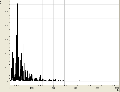
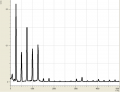
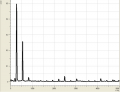
Allgemein haben wir bei den verschiedenen Tönen beobachten können, dass sie sowohl aus wenigen (bis zu einem), als auch aus vielen (bei uns waren es bis zu 6) Obertönen bestehen können. So bestand z.B. ein mit dem Mund erzeugtes "a" aus etwa 5 Obertönen, die sich in dem Bereich um 2000Hz verteilten. Hingegen kennzeichnete sich ein "a", welches mit dem Fagott gespielt wurde durch eigentlich nur einen Oberton bei 1000Hz aus. Senken wir jedoch die Frequenz, erkennen wir ein häufigeres Auftreten von Obertönen.
Spektren eines Fagotts
- Spektren eines Fagotts
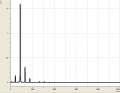
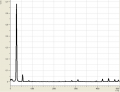
Spektren gesungener Vokale
- Gesungene Vokale
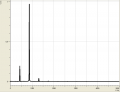
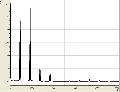
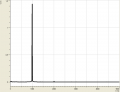
Stimmgabel und Rauschen
Weiterhin sind wir noch auf zwei extreme Spezialfälle gestoßen: Einmal betrachteten wir eine Stimmgabel, welche sehr wenig Obertöne besaß. Der Amplitude des großen Obertons wurde eine Frequenz von ziemlich genau 1000Hz zugeordnet. Anderseits betrachteten wir "Rauschen", welches sich, wie wir sahen, durch viele Obertöne, also durch relativ hohe Amplituden bei möglichst jeder Frequenz, kennzeichnet.
Erklärung
Das Frequenzspektrum hat uns also Auskunft über die harmonischen Schwingungen der versch Töne gegeben und gezeigt dass ein Ton, den wir als einen Ton wahr nehmen nicht immer nur aus einer Schwingung besthet. Bei der Stimmgabel sehen wir jedoch genau eine Schwingung (die anderen analysierten Töne seien vernachlässigt, entstehung vielleicht durch Geräusche im Raum). Das ist hierbei aber ziemlich unbeeindruckend, da sie dafür gebaut ist Musikinstrumente zu stimmen und genau auf 1000Hz geeicht ist. Das Gegenextrem zu einem Oberton ist, wie schon in der Beobachtung gesehen, das Rauschen. Auch hier gibt es eine Besonderheit, und zwar wenn jeder Frequenz die gleiche Amplitude zugeordnet wird nennt man das: Weisses Rauschen.