Experimentelle Untersuchung einer Schaukel: Unterschied zwischen den Versionen
(→Erklärung/Auswertung) |
(→Erklärung/Auswertung) |
||
| Zeile 114: | Zeile 114: | ||
<br/>Nur bei <math>\sqrt {l}</math> sind Züge einer Übereinstimmung zu erkennen. Somit lässt sich sagen, dass sich die Wurzel der Länge proportional zur Periode verhält (<math>\sqrt l \propto T</math>). | <br/>Nur bei <math>\sqrt {l}</math> sind Züge einer Übereinstimmung zu erkennen. Somit lässt sich sagen, dass sich die Wurzel der Länge proportional zur Periode verhält (<math>\sqrt l \propto T</math>). | ||
| − | Versuche: ''Johannes Schlicksbier'' und ''Nikolaj Kulvelis'' | + | <div>align="right"Versuche: ''Johannes Schlicksbier'' und ''Nikolaj Kulvelis'' |
| − | <br/>Onlineausarbeitung: ''Nikolaj Kulvelis'' | + | <br/>Onlineausarbeitung: ''Nikolaj Kulvelis''</div> |
Version vom 28. September 2006, 22:40 Uhr
Inhaltsverzeichnis
Vorüberlegungen
Zu untersuchen:
- Wie man antreibt
- Wirken von Kräften
- Beschreiben der Bewegung
- Impulsfluss
- Abhängigkeit der Bewegung
- Energiemengen/Fluss (zB Wärme)
Beschreibung der Bewegung:
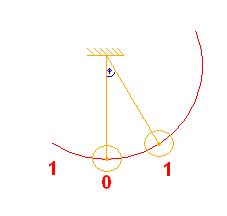
Vereinfachung als Fadenpendel (mathematischer Pendel)
Koordinatensystem
Angabe des Ortes
durch y:Elongation
Bei y=0: Pendel in Ruhelage
Messen der Elongation mit Hilde des Winkels [math]\varphi[/math]
Weitere Vereinfachung: Ungedämpftes Pendel (Ohne Energieverlust)
Maximale Auslenkung: [math]\hat y[/math](Amplitude)
Periode(ndauer)T: Zeit einer Schwingung
Frequenz f: Anzahl Schwingungen pro Zeit
[ T=1/f | f=1/T ]
Wovon hängt die Frequenz der frei schwingenden Schaukel ab?
- Fadenlänge l
- Masse m
- Amplitude [math]\hat y[/math]
- Reibung
Periodenlänge eines Fadenpendels
Aufbau:
Text Text Text Text Text Text TextText Text Text Text Text Text Text Text Text Text Text
Beobachtung/Messwerte:
Abhängigkeit von der Fadenlänge l:
Tabelle 1 [math]m[/math] = 0,1342 kg; [math]\hat y[/math] = 30° [math]l[/math] | 10 cm | 20 cm | 30 cm | 40 cm | 50 cm [math]T[/math] | 0,774 s | 1s | 1,16 s | 1,29s | 1,506 s
Abhängigkeit von der Amplitude [math]\hat y[/math]:
Tabelle 2 [math]m[/math] = 0,1342 kg; [math]l[/math] = 30 cm [math]\hat y[/math] | 15° | 30° | 45° | 60° | 75° | 90° [math]T[/math] | 1,106 s | 1,16 s | 1,158 s | 1,188s | 1,244s | 1,366s
Text Text Text Text Text Text TextText Text Text Text Text Text Text Text Text Text Text
Erklärung/Auswertung
Text Text Text Text Text Text TextText Text Text Text Text Text Text Text Text Text Text
Periodenlänge einer schwingenden Stange
Aufbau:
Text Text Text Text Text Text TextText Text Text Text Text Text Text Text Text Text Text
Beobachtung/Messwerte:
Abhängigkeit von der Amplitude [math]\hat y[/math]:
Tabelle 1 [math]m[/math] = 1.01kg; [math]l[/math] = 1.01m [math]\hat y[/math] | 30° | 45° | 90° | [math]T[/math] | 1.64s | 1.69s | 1.92s |
Tabelle 2 [math]m[/math] = 0.23kg; [math]l[/math] = 1.06m [math]\hat y[/math] | 30° | 45° | 90° | [math]T[/math] | 1.69s | 1.77s | 1.98s |
Tabelle 3 [math]m[/math] = 0.31kg; [math]l[/math] = 0.33m [math]\hat y[/math] | 30° | 45° | 90° | [math]T[/math] | 0.98s | 1s | 1.11s |
Während der Versuchsdurchführung können wir an unserer Stativstange ein gewisses "Mitschwingen" beobachten, im Takt zum eigentlich schwingenden Objekt.
Weiterhin ist noch hinzuzufügen, dass die maximale Elongation von Periode zu Periode um ein sehr unterschiedliches Maß abnimmt, die Differenzen werden immer kleiner. Da wir dies bei all unseren Testreihen beobachten, testen wir abgesondert den "Extremfall", eine Amplitude von 180°, um diesen Effekt zu verstärken. Hierbei können wir beobachten, dass bereits nach einer Periode die Differenz der Amplitude etwa 60° beträgt; nach der zweiten 30°, usw.
Erklärung/Auswertung
Wie aus den Tabellen 1 und 2 zu entnehmen ist, haben unsere Stangen eine sehr ähnliche Länge ([math]l[/math]), jedoch eine unterschiedliche Masse: Stange 2 wiegt weniger als ein Viertel von Stange 1. Hiermit können wir Johannes' anfängliche Hypothese, dass die Masse ([math]m[/math]) irrelevant sei, sehr gut untermauern. Für die einzelnen Amplituden ([math]\hat y[/math]) weichen die Perioden ([math]T[/math]) jeweils nur um ein paar Hunderstelsekunden voneinander ab. "Ein solch geringer Unterschied hat seinen Ursprung nicht in einer so großen Massenrelation von 1:4" denken wir uns; die geringfügigen Längenunterschiede und Messungenauigkeiten müssen hierfür verantwortlich sein.
An dieser Stelle kommt Stange 3 ins Spiel, mit einer dritten Länge. Somit lässt sich die Abhängigkeit der Periode von der Länge besser untersuchen: auf den ersten Blick ist klar, dass die Periode mit Zunahme der Länge ebenfalls zunimmt ([math]l \propto T[/math]?). Um die genaue Abhängigkeit herauszufinden, probieren wir gängige Verhältnisse mithilfe einer allgemeinen Formel aus:
([math]c[/math] steht für die restlichen Bestandteile der Schwingungsformel; die Rechnungen gelten für [math]\hat y=45[/math]°)
- [math]T = l c[/math]
- [math]T \over l[/math][math] = c[/math] ; [math]1.77 \over l.06[/math][math] = 1.67[/math] ; [math]1.69 \over 1.01[/math][math] = 1.67[/math] ; [math]1 \over 0.33[/math][math] = 3.03[/math]
- [math]T = l^2 c[/math]
- [math]T \over l^2[/math][math] = c[/math] ; [math]1.77 \over 1.06^2[/math][math] = 1.56[/math] ; [math]1.69 \over 1.01^2[/math][math] = 1.66[/math] ; [math]1 \over 0.33^2[/math][math] = 9.18[/math]
- [math]T = \sqrt{l} c[/math]
- [math]c=[/math][math] T \over \sqrt{l}[/math] ; [math] 1.77 \over \sqrt{1.06}[/math][math]=1.71[/math] ; [math] 1.69 \over \sqrt{1.01}[/math][math]=1.68[/math] ; [math] 1 \over \sqrt{0.33}[/math][math]=1.74[/math]
Nur bei [math]\sqrt {l}[/math] sind Züge einer Übereinstimmung zu erkennen. Somit lässt sich sagen, dass sich die Wurzel der Länge proportional zur Periode verhält ([math]\sqrt l \propto T[/math]).
Onlineausarbeitung: Nikolaj Kulvelis