Die Feldstärke als gerichteter Ortsfaktor: Unterschied zwischen den Versionen
K (→Messen der Feldstärke eines Kondensators) |
|||
| Zeile 136: | Zeile 136: | ||
\Rightarrow & F_e & \approx & F_g \, \frac{a}{l} = m\, g \, \frac{a}{l} \\ | \Rightarrow & F_e & \approx & F_g \, \frac{a}{l} = m\, g \, \frac{a}{l} \\ | ||
& & = & 0{,}51\!\cdot\! 10^{-3}\rm kg \cdot 9{,}8\frac{N}{kg} \, \frac{2\,\rm cm}{40\,\rm cm} \\ | & & = & 0{,}51\!\cdot\! 10^{-3}\rm kg \cdot 9{,}8\frac{N}{kg} \, \frac{2\,\rm cm}{40\,\rm cm} \\ | ||
| − | & & = & 2{,}499\!\cdot\! 10^{- | + | & & = & 2{,}499\!\cdot\! 10^{-4}\rm N \approx 0{,}25\,\rm mN\\ |
\end{array} | \end{array} | ||
| Zeile 142: | Zeile 142: | ||
Der Quotient aus Kraft und Ladung ist die Feldstärke: | Der Quotient aus Kraft und Ladung ist die Feldstärke: | ||
| − | :<math>E=\frac{F}{q}=\frac{2{,}499\!\cdot\! 10^{- | + | :<math>E=\frac{F}{q}=\frac{2{,}499\!\cdot\! 10^{-4}\rm N}{1\!\cdot\! 10^{-9}\rm C}=249900 \,\rm \frac{N}{C}</math> |
==[[Aufgaben zu den Grundlagen über Felder#Feldstärke|Aufgaben]]== | ==[[Aufgaben zu den Grundlagen über Felder#Feldstärke|Aufgaben]]== | ||
Aktuelle Version vom 18. Oktober 2022, 15:17 Uhr
(Kursstufe > Grundlagen elektrischer, magnetischer und schwerer Felder)
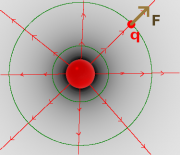
Um die Stärke und Struktur eines Feldes zu untersuchen, benutzt man sogenannte Probekörper und misst die Kraftwirkung. Eine große Kraft an einer Stelle läßt auf ein dort "starkes" oder "dichtes" Feld schließen. Die Richtung der Kraft zeigt die lokale Struktur des Feldes an.
Gravitationsfelder untersucht man mit einem Gegenstand, der eine Masse hat (Welcher hat das nicht ;), elektrische Felder mit einem positiv geladenen Gegenstand und Magnetfelder mit einem isolierten Nordpol, den man experimentell durch eine große Entfernung zum Südpol erreichen kann.
Das zu untersuchende Feld verändert sich allerdings durch den Probekörper. Diese Veränderung des Feldes ist klein, wenn der Probekörper "klein" ist, also zB. eine kleine Masse hat[1]. Daher betrachtet man den Grenzwert für immer kleinere Ladungen. Bei halber Ladung des "kleinen" Probekörpers, ist auch die gemessene Kraftwirkung halb so groß. Der Quotient aus Kraft und Ladung ist also konstant und eine vom Probekörper unabhängige Feldeigenschaft, die man Feldstärke nennt. Sie gibt die auf eine Ladungseinheit normierte Kraftwirkung auf einen "infinitesmal kleinen" Probekörper an. Bei realen Probekörpern gibt es eine mehr oder weniger große Abweichung.
Somit wird jeder Stelle des Feldes eine Feldstärke in Betrag und Richtung zugeordnet, was man mathematisch auch Vektorfeld nennt. Dieses Vektorfeld beschreibt eine Eigenschaft des Feldes und ist nicht das Feld selbst.
Inhaltsverzeichnis
Beispiele
Darstellung der Stärke der Gravitation auf der Erde. (animiert)
Video: Vermessung der Gravitation
Versuche zur Feldstärke
Eine Federwaage im Gravitationsfeld
Aufbau
Man hängt ein Gewicht an eine Feder.
Beobachtung
Die Feder dehnt sich und hängt nach unten, bei zwei Gewichten ist die Verlängerung der Feder auch doppelt so groß. (Sie wird auf Meereshöhe, auf dem Mount Everest oder auf dem Mond unterschiedlich stark gedehnt.)
Erklärung
- Die wirkende Kraft ist proportional zur schweren Masse des Probekörpers, bei halber Masse ist die Kraft auch halb so groß: [math]F \sim m [/math]
- Macht man die Masse des Probekörpers immer kleiner, so wird das Gravitationsfeld immer weniger gestört. Dabei bleibt aber das Verhältnis von Kraft und Masse konstant.
- Die Kraft pro Masse ("normierte Kraftwirkung") ist also nur vom Ort abhängig und ein Maß für die Stärke des Feldes.[2][3]
Die Feldstärke des Gravitationsfeldes ist der Ortsfaktor [math]\vec g=\frac{\vec F}{m}\quad \left(\Leftrightarrow \vec F= m\ \vec g \right)[/math]
mit der Einheit [math][\vec g]=\mathrm{ \frac{1\, N}{1\, kg} }[/math].Sie gibt die normierte Kraftwirkung auf ein Kilogramm Masse an.
Vermessung eines Magnetfeldes
Aufbau
Der Nordpol eines langen Stabmagnets ist an einem Kraftsensor befestigt. Man bringt den Nordpol in das Feld eines anderen Stabmagneten und misst die auftretenden Kräfte in Stärke und Richtung. (Der Sensor misst die immer nur die Kraftkomponente in einer Richtung.)
Man "verdoppelt" den Probenordpol durch einen zweiten Stabmagneten.
Beobachtung
- Bei der halben Probeladung misst man die halbe Kraftwirkung: [math]F \sim q_m[/math][4]
- Verkleinert man die Ladung des Nordpols immer weiter, so wird das zu untersuchendende Magnetfeld immer weniger gestört. Dabei bleibt aber das Verhältnis von Kraft und magnetischer Ladung konstant.
- Die Kraft pro magnetischer Ladung ("normierte Kraftwirkung") ist also nur vom Ort abhängig und ein Maß für die Stärke des Feldes.
Die Feldstärke des Magnetfeldes ist der Ortsfaktor [math]\vec H=\frac{\vec F}{q_m} \quad \left(\Leftrightarrow \vec F= q_m\ \vec H \right)[/math]
mit der Einheit [math][ \vec H] = {\rm \frac{1\, N}{1\, Wb} = \frac{1\, N}{1\, V\,s} = \frac{A}{m}}[/math].
Sie gibt die normierte Kraftwirkung auf einen Weber magnetische Ladung an
Hier bleibt zunächst die Frage offen, wie man magnetische Ladungen messen soll. Dies gelingt erst, indem man mit Hilfe des Magnetfeldes einer stromdurchflossenen Spule die magnetische Feldstärke festlegt. Man kann also die obige Definition der magnetischen Feldstärke als Definition der magnetischen Ladung interpretieren.
Auch der Sinn der Einheit Ampère pro Meter wird erst im Zusammenhang mit elektrischen Strömen klar.
Vermessung eines elektrischen Feldes
Aufbau
Zwei Kugeln, aufladen, Kraft mit Sensor messen, Ladung über abfließenden Strom mit Messverstärker. ACHTUNG!! Es ist nicht ratsam in der Nähe des CASSY-Messgerätes mit hohen Spannungen zu experimentieren. Die Elektronik kann zerstört werden![5]
Beobachtung
- Bei der halben Probeladung misst man die halbe Kraftwirkung: [math]F \sim q[/math][4]
Erklärung
- Die Kraft pro elektrischer Ladung ("normierte Kraftwirkung") ist also nur vom Ort abhängig und ein Maß für die Stärke des Feldes.
Die Feldstärke des elektrischen Feldes ist der Ortsfaktor [math]\vec E =\frac{\vec F}{q} \quad \left(\Leftrightarrow \vec F= q\ \vec E \right)[/math]
mit der Einheit [math][\vec E]=\mathrm{ \frac{1\, N}{1\, C} = \frac{1\, N}{1\, A\,s} = \frac{1\, V}{1\, m} }[/math].
Sie gibt die normierte Kraftwirkung auf ein Coulomb elektrische Ladung an.
Der Sinn der Einheit Volt pro Meter wird erst klar, wenn man sich mit dem Potential eines Feldes beschäftigt.
Messen der Feldstärke eines Kondensators
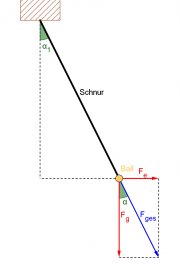
AufbauEin Kondensator wird an eine Hochspannungsquelle angeschlossen. In seinem elektrischen Feld hängt eine bifilar aufgehängte Rasierklinge. Man berührt dann mit der Klinge eine der Kondensatorplatten und läßt die Klinge wieder frei hängen.
Beobachtung und Messung
Die Rasierklinge hängt nach der Berührung mit einer Platte nicht mehr senkrecht nach unten, sie nähert sich der anderen Platte.
Mit einem Messverstärker bestimmt man die auf der Klinge sitzende Ladung zu [math]q= 1\,\rm nC[/math].
Mit Hilfe einer Schattenprojektion bestimmt man die Fadenlänge zu [math]l=40\,\rm cm[/math] und die Auslenkung zu [math]a=2\,\rm cm[/math].
Mit einer Waage bestimmt man die Masse der Klinge zu [math]m= 0{,}51\,\rm g[/math].
Ergebnis
Die Rasierklinge ist ein Probekörper im Feld des Kondensators. Durch die Berührung lädt sich die Klinge positiv (negativ) auf. Vom elektrischen Feld wird sie daher in (gegen die) Richtung der Feldlinien gezogen, zur negativ (positiv) geladenen Platte hin.
Die Masse liefert uns die Gewichtskraft [math]F_g[/math] der Klinge. Durch den Auslenkungswinkel kann man daraus die horizontal auf die Klinge wirkende elektrische Kraft [math]F_e[/math] berechnen, denn die Summe der Gewichtskraft und elektrischen Kraft muss parallel zum Faden wirken:
[math] \begin{array}{rrcl} & \frac{F_e}{F_g} & = & \tan \alpha \approx \frac{a}{l} \qquad |\cdot F_g\\ \Rightarrow & F_e & \approx & F_g \, \frac{a}{l} = m\, g \, \frac{a}{l} \\ & & = & 0{,}51\!\cdot\! 10^{-3}\rm kg \cdot 9{,}8\frac{N}{kg} \, \frac{2\,\rm cm}{40\,\rm cm} \\ & & = & 2{,}499\!\cdot\! 10^{-4}\rm N \approx 0{,}25\,\rm mN\\ \end{array} [/math]
Der Quotient aus Kraft und Ladung ist die Feldstärke:
- [math]E=\frac{F}{q}=\frac{2{,}499\!\cdot\! 10^{-4}\rm N}{1\!\cdot\! 10^{-9}\rm C}=249900 \,\rm \frac{N}{C}[/math]
Aufgaben
Fußnoten
- ↑ "But if the body is very small and its charge also very small, the electrification of the other bodies will not be sensibly disturbed, and we may consider the body as indicating by its centre of gravity a certain point of the field. The force acting on the body will then be proportional to its charge, and will be reversed when the charge is reversed." (Maxwell: A Treatise on Electricity and Magnetism, Chapter One, Description of phenomena, [44] ) BAUSTELLE: (Oder Ladung gleichmäßig in Kugelform verteilt.) Verweis auf Berechnung mit dem Feldfluss "Das Außenfeld einer homogen geladenen Kugel ist gleich dem einer Punktladung im Mittelpunkt der Kugel ([1])"
- ↑ Durch die Drehung der Erde misst man auf der Erdoberfläche nicht überall die gesamte Gravitationswirkung. Streng genommen ist deshalb der Ortsfaktor geringfügig kleiner als die Gravitationsfeldstärke, vor allem am Äquator.
- ↑ Aus dem konstanten Quotienten von Kraft und Masse folgt überraschenderweise, dass es für die Messung der Feldstärke keine Rolle spielt, welche Masse der Probekörper hat. Man muss sich aber klarmachen, dass man die Feldstärke des ungestörten Feldes gemessen hat, auch wenn sich das Feld durch den "großen" Probekörper verändert. So könnte man die Erde als Probekörper im Gravitationsfeld eines Apfels interpretieren. Als Ergebnis erhält man die Feldstärke des Apfels, so wie sie ohne der Anwesenheit der Erde wäre!
Das spielt bei der Berechnung der Kraftwirkung zwischen zwei Kondensatorplatten eine große Rolle. - ↑ 4,0 4,1 Die Probeladung wird mit einem kleinen Buchstaben notiert, um sie von der felderzeugenden Ladung zu unterscheiden.
- ↑ Vgl. CASSY-Handbuch, S.190
Links
- Wikipedia: Magnetostatik Hier wir die magnetische Polstärke angesprochen.
- Wikipedia: magnetische Monopole
- euronews space : Wie die Schwerkraft die Erde fest im Griff hat
- Gravimetrie (Schwerkraft-Messungen, Messungen der Schwere) (Prof. Dr. Dr. habil. Kord Ernstson, Universität Würzburg)