Formatvorlagen
Inhaltsverzeichnis
Text formatieren
kein Inhaltsverzeichnis: __NOTOC__
Keine Abschnittsbearbeitung: __NOEDITSECTION__
Eine echte Leerzeile hinter einem Bild: <br style="clear: both" />
Hoch- und Tiefgestellte Zeichen:
<sup>hochgestellt</sup>
Text hochgestellt
<sub>tiefgestellt</sub>
Text tiefgestellt
Eine Fußnote
Hier ist noch Folgendes zu Erwähnen. [1]
<ref>Fußnote</ref>
Und nach dem Text steht ganz unten:
- ↑ Fußnote
<references />
Mehrere Verweise auf die gleiche Fußnote:
Erster Verweis:
<ref name="Name">Fußnotentext</ref>
Nächste Verweise:
<ref name="Name" />
Ein wichtiger Merksatz
{|class="wikitable" style="border-style: solid; border-width: 4px "
|
ES GIBT NICHTS GUTES, AUSSER MAN TUT ES!
|}
|
ES GIBT NICHTS GUTES, AUSSER MAN TUT ES! |
Eine Datei zum Runterladen
[[media:Beurteilungsbogen_GFS.pdf|Bewertungsmaßstäbe]] einer GFS
- Bewertungsmaßstäbe einer GFS
Ein Zitat
"War es ein Gott, der diese Zeichen schrieb,
Die mit geheimnißvoll verborg'nem Trieb
Die Kräfte der Natur um mich enthüllen,
Und mir das Herz mit stiller Freude füllen."[1]
Bilder
Copyrightangabe bei eigenen Bildern
By Patrick Nordmann (schulphysikwiki.de)
[https://creativecommons.org/licenses/by-sa/4.0/]
Bild in Hochkant Voransicht
[[Datei:Luftkissenpuck Fußball Schnur Hand.jpg|thumb|upright]]
Eine Tabelle mit Bildern
<gallery widths=200px heights=150px perrow=4 caption="Spiegelbild einer Lampe in einer Seifenhaut">
Bild:film_of_soap_interference_1.jpg|Bild 1 <br /> ...und ein Kommentar in einer neuen Zeile
Bild:Eisschnellläuferin.jpg|<ref>Ausschnitt aus einem [http://commons.wikimedia.org/wiki/File:Svetlana_Vysokova_-_5000m_speed_skating_-_Vancouver_2010.jpg Bild von Robert Scoble]-CC BY 2.0</ref> Noch schneller geht es mit Schlittschuhen.
Bild:|
Bild:|
Bild:|
</gallery>
- Spiegelbild einer Lampe in einer Seifenhaut
[2] Noch schneller geht es mit Schlittschuhen.
Tabellen
Eine Tabelle mit Text nach oben ausgerichtet
Mit |style="vertical-align:top;"|
|
An einem Wasserkraftwerk an der Dreisam finden sich folgende Angaben:
Man kann aus Durchfluss und Fallhöhe die maximale Leistung berechnen:
Die Turbine hätte demnach einen sehr hohen Wirkungsgrad! |
Eine vom Text umflossene Tabelle
{|style="float:right;"
|valign="top"|
Erste Spalte
|valign="top"|
Zweite Spalte
|}
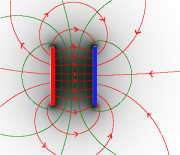
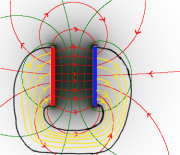
Ein homogenes Feld ist, wie der Name schon sagt, überall gleich. Das heißt, seine Dichte/Stärke und seine Struktur (Richtungen) sind überall gleich.
- Ein Kondensator mit großen Platten und kleinem Abstand hat ein fast homogenes Feld zwischen den Ladungen.
- Ein kurzer Magnet mit großflächigen Polen, wie ein Scheibenmagnet ebenso.
- Es gibt keinen "Gravitationskondensator", da es nur positive Massen gibt.
- Das Gravitationsfeld ist in dem uns vertrauten Bereich von ca. 10 km Breite, Länge und Höhe fast homogen. (Alle Felder ohne Sprünge oder Knicke sind in einem kleinen Ausschnitt fast homogen!)
- Das elektrische/magnetische Feld zieht die Platten/Pole aufeinander zu. Senkrecht dazu zieht es die einzelnen Platten/Pole in die Länge.
- Bei einem Plattenkondensator werden deshalb die Ladungen an die Innenseite der Platten gezogen und gleichzeitig quer zu den Feldlinien an die äußeren Ränder der Platten gedrückt.
eine schöne Tabelle mit Rand
{|class="wikitable" style="text-align: center"
!style="border-style: solid; border-width: 4px "|
Überschrift 1
!valign="top"; style="border-style: solid; border-width: 4px "|
Überschrift 2
|-
|style="border-style: solid; border-width: 4px "|
Zeile 1 Spalte 1 etwas breiter
|style="border-style: solid; border-width: 4px "|
Zeile 1 Spalte 2
|-
|style=" text-align:right; border-style: solid; border-width: 4px "|
rechts: Zeile 2 Spalte 1
|valign="top"; style="border-style: solid; border-width: 4px "|
Zeile 2 Spalte 2
|-
|style="text-align:left; border-style: solid; border-width: 4px "|
links: Zeile 3 Spalte 1
|valign="top"; style="border-style: solid; border-width: 4px "|
Zeile 3 Spalte 2
|}
|
Überschrift 1 |
Überschrift 2 |
|---|---|
|
Zeile 1 Spalte 1 etwas breiter |
Zeile 1 Spalte 2 |
|
rechts: Zeile 2 Spalte 1 |
Zeile 2 Spalte 2 |
|
links: Zeile 3 Spalte 1 |
Zeile 3 Spalte 2 |
Eine elegante Tabelle mit dünnem Rand
{|class="wikitable"
!Name der Energie
!colspan="2"|Mengenartige (extensive) Größen
(Energieträger)
!colspan="2"|haben zugehörige Eigenschaften (intensive Größen)
(Potential / Beladungsmaß)
!Leistung
[math]P = \dot E[/math]
!absolute
Energieänderung
!gespeicherte
Energie
|-
|
|align="right"|Energie
|[math][E]=\mathrm{J \quad(Joule)}[/math]
|colspan="5"|
|-
|elektrische Energie
|align="right"|el. Ladung
|[math][Q] = \mathrm{C \quad (Coulomb)}[/math]
|align="right"|el. Potential
|[math][\varphi_{el}] = \mathrm{V \quad (Volt)}=\frac{J}{C}[/math]
|[math]P=\varphi \, I \quad (U\, I)[/math]
|[math]\triangle E = \varphi \, Q \quad (U \, Q)[/math]
|[math]E= \bar \varphi \, Q \quad (\bar U \, Q)[/math]
|}
| Name der Energie | Mengenartige (extensive) Größen (Energieträger) |
haben zugehörige Eigenschaften (intensive Größen) (Potential / Beladungsmaß) |
Leistung [math]P = \dot E[/math] |
absolute Energieänderung |
gespeicherte Energie | ||
|---|---|---|---|---|---|---|---|
| Energie | [math][E]=\mathrm{J \quad(Joule)}[/math] | ||||||
| elektrische Energie | el. Ladung | [math][Q] = \mathrm{C \quad (Coulomb)}[/math] | el. Potential | [math][\varphi_{el}] = \mathrm{V \quad (Volt)}=\frac{J}{C}[/math] | [math]P=\varphi \, I \quad (U\, I)[/math] | [math]\triangle E = \varphi \, Q \quad (U \, Q)[/math] | [math]E= \bar \varphi \, Q \quad (\bar U \, Q)[/math] |
Tabelle mit mehr Rand in den Zellen
{|style="border-collapse: separate; border-spacing: 30px 0px;"
|
a) [math]\int_0^2 \!\! f(x)\,dx[/math]
|
b) [math]\int_0^{3.9}\!\! f(x)\,dx[/math]
|
c) [math]\int_{3.9}^{6.2}\!\! f(x)\, dx[/math]
|}
|
a) [math]\int_0^2 \!\! f(x)\,dx[/math] |
b) [math]\int_0^{3.9}\!\! f(x)\,dx[/math] |
c) [math]\int_{3.9}^{6.2}\!\! f(x)\, dx[/math] |
Mathe
Ein Doppelpunkt in einer Formel: 20 \, \colon 5 = 4 ergibt: [math]20 \, \colon 5 = 4[/math]
In einem Fließtext braucht man nur die [math]\tfrac{1}{2}[/math] Größe: \tfrac{1}{2}
Eine mathematische Gleichungsumformung / Herleitung
\begin{align}
h &= \sqrt[12]{2} \\
f(x,y,z) &= x + y + z
\end{align}
|
[math] \begin{align} h &= \sqrt[12]{2} \\ f(x,y,z) &= x + y + z \end{align} [/math] |
\begin{alignat}{2}
a\, b &= z & \quad | :b \quad \text{teilen} \\
\Rightarrow \quad a &= \frac{z}{b}
\end{alignat}
|
[math] \begin{alignat}{2} a\, b &= z & \quad | :b \quad \text{teilen} \\ \Rightarrow \quad a &= \frac{z}{b} \end{alignat} [/math] |
\left. \begin{align}
c_L &=\lambda_L \,f \\
c &=\lambda \,f
\end{align} \ \right\} \Rightarrow \
\frac{c_L}{c}=\frac{\lambda_L}{\lambda}
|
[math]\left.\begin{align} c_L &=\lambda_L \,f \\ c &=\lambda \,f \end{align}\ \right\} \Rightarrow \ \frac{c_L}{c}=\frac{\lambda_L}{\lambda} [/math] |
\text{aus } 2\,x=8 \text{ folgt: } x=4
|
[math] \text{aus } 2\,x=8 \text{ folgt: } x=4 [/math] |
\begin{array}{rcl}
h &=& \sqrt[12]{2} \\
f(x,y,z) &=& x + y + z
\end{array}
|
[math] \begin{array}{rcl} h &=& \sqrt[12]{2} \\ f(x,y,z) & = & x + y + z \end{array} [/math] |
\begin{array}{rrcll}
& a\, b &=& z & | :b \quad \text{teilen} \\
\Rightarrow & a &=& \frac{z}{b}
\end{array}
|
[math] \begin{array}{rrcll} & a\, b & = & z & | :b \quad \text{teilen} \\ \Rightarrow & a & = & \frac{z}{b} \end{array} [/math] |
Merksatz mit Formeln und Einheiten
{|class="wikitable" style="border-style: solid; border-width: 4px "
|
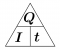
Fließt elektrische Ladung, so gibt die Stromstärke [math]I[/math] an wieviel Ladung [math]Q[/math] an einer Stelle pro Zeit [math]t[/math] durchfließt. Sie wird in Coulomb pro Sekunde oder Ampère gemessen:
|} |}
|
Fließt elektrische Ladung, so gibt die Stromstärke [math]I[/math] an wieviel Ladung [math]Q[/math] an einer Stelle pro Zeit [math]t[/math] durchfließt. Sie wird in Coulomb pro Sekunde oder Ampère gemessen:
|
Verschiedene mathematische Schriftarten
\mathrm {P = U\, I} oder \rm P = U\, I
\mathcal {P = U\, I}
\mathbf {P = U\, I}
\mathsf {P = U\, I}
\mathit {P = U\, I}
\mathtt {P = U\, I}
|
[math] \begin{align} \mathrm {P = U\, I} \text{ oder } \rm P = U\, I \\ \mathcal{P = U\, I} \\ \mathbf {P = U\, I} \\ \mathsf {P = U\, I} \\ \mathit {P = U\, I} \\ \mathtt {P = U\, I} \\ \end{align} [/math] |
Bunte Formeln
(Liste der vordefinierten Farben, "\definecolor" klappt leider nicht.)
P( \color{blue}{-2 } | \color{red}{1} )
|
[math] P( \color{blue}{-2} | \color{red}{1} ) [/math] |
Brüche kürzen
6\,\rm V \cdot 0{,}5\rm A
= 6\,\rm \frac{J}{C\!\!\!\! /} \cdot 0{,}5\rm \frac{C\!\!\!\! /}{s}
= 3\,\rm \frac{J}{s} = 3\,\rm W
|
[math] 6\,\rm V \cdot 0{,}5\rm A = 6\,\rm \frac{J}{C\!\!\!\! /} \cdot 0{,}5\rm \frac{C\!\!\!\! /}{s} = 3\,\rm \frac{J}{s} = 3\,\rm W[/math] |
Das Gradzeichen
0^{\circ}C \hat = 273{,}15\,\rm K
|
[math] 0^{\circ}\rm C \ \hat = \ 273{,}15\,\rm K [/math] |
Integrale
\int_0^1 x^2 \,\mathrm{d}x = \left[\tfrac{1}{3}x^3\right]_0^1
|
[math] \int_0^1 x^2 \,\mathrm{d}x = \left[\tfrac{1}{3}x^3\right]_0^1 [/math] |
\int\limits_0^1 x^2 \,\mathrm{d}x = \left[\tfrac{1}{3}x^3\right]_0^1
|
[math] \int\limits_0^1 x^2 \,\mathrm{d}x = \left[\tfrac{1}{3}x^3\right]_0^1 [/math] |
Vektoren und Matrizen
\begin{pmatrix} 1 \\ 2 \end{pmatrix}
|
[math]\begin{pmatrix} 1 \\ 2 \end{pmatrix}[/math] |
\left[\vec x - \begin{pmatrix} 1 \\ 2 \\ 3\end{pmatrix}\right]
\cdot \begin{pmatrix} 4 \\ 5 \\ 6\end{pmatrix} = 0
|
[math]\left[\vec x - \begin{pmatrix} 1 \\ 2 \\ 3\end{pmatrix}\right] \cdot \begin{pmatrix} 4 \\ 5 \\ 6\end{pmatrix} = 0 [/math] |
\begin{pmatrix}
11 & 12 \\
21 & 22
\end{pmatrix}
|
[math]\begin{pmatrix} 11 & 12 \\ 21 & 22 \end{pmatrix}[/math] |
Inhalte einbinden
Animationen aus geogebra.org einbinden
(Zur [https://www.geogebra.org/material/show/id/z3kkenvr Datei] und zum [https://www.geogebra.org/download?lang=de Programm])
{{#widget:Iframe
|url=https://www.geogebra.org/material/iframe/id/qyxcfjgt/width/880/height/481/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false
|width=880
|height=481
|border=0
}}
Ein Video von dailymotion einbinden
{{#widget:Iframe
|url=https://www.dailymotion.com/embed/video/x7sxzti?queue-enable=false&ui-logo=false
|width=640
|height=360
|border=0
}}
- Keine Weiterleitung am Ende und ohne Logo (Link):
?queue-enable=false&ui-logo=false
Ein Video von youtube
Mit: <youtube>8wN2y94N3GI</youtube>
Ein Geogebra-Bild im richtigen Maßstab
Bei 96dpi und 100% Druckgröße wird ein Zentimeter auch einen Zentimeter lang!
Test_4x6cm_96dpi.png
Links
- Landesbildungsserver Baden-Württemberg: Der elektrische Schwingkreis
- Walter Fendt: Applet zum Schwingkreis
- Telekolleg: Vergleich elektrischer Schwingkreis mit Federschwingung
Fußnoten
- ↑ Ein abgewandeltes Faust-Zitat von Ludwig Boltzmann über die Maxwellschen Gleichungen, aus: Vorlesungen, II Teil, Vorwort, zitiert nach [Sim] , S.347
- ↑ Ausschnitt aus einem Bild von Robert Scoble-CC BY 2.0