Aufgaben zum Elektro-Magnetismus

Magnetfelder um Ströme (Ampèrsches Gesetz)

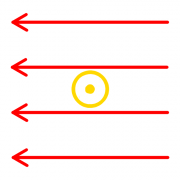
Magnetfeld von Kabel und Spule

Zeichnen Sie jeweils einige Feldlinien und Flächen ein.

• 

  a) Ein stromdurchflossenes Kabel.

• 

  b) Eine stromdurchflossene Spule.

Magnetische Feldstärke

a) Wie wurde die schwere, elektrische und magnetische Feldstärke bereits mit Hilfe einer Probeladung definiert?

b) Warum ist diese Festlegung im elektrischen und schweren Fall praktikabel, aber im magnetischen Fall nicht?

c) Wie wird daher die magnetische Feldstärke definiert?

Feldstärken berechnen

a) Eine Spule ist 60cm lang, hat einen Durchmesser von 15cm und 2000 Windungen. Es fließt ein Strom der Stärke 300mA durch das Kabel.

Berechnen Sie die magnetische Feldstärke innerhalb der Spule.

b) Ist es egal, ob die Spule einen Durchmesser von 15cm oder von 30cm hat?

c) Durch ein Kabel fließt ein Strom mit der Stärke von 20 Ampère.

Berechnen Sie die magnetische Feldstärke in einem Abstand von 1cm, 2cm und 3cm vom Kabel.

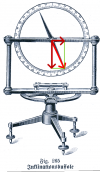
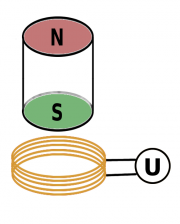
Horizontalkomponente des Erdmagnetfeldes

Ein Inklinationskompass mit eingezeichneten Komponenten des Erdmagnetfeldes.

Die Feldlinien des Erdmagnetfeldes verlaufen nur am Äquator parallel zur Erdoberfläche und in geographischer Süd-Nord-Richtung. In Deutschland bilden die Feldlinien mit dem Erdboden einen sogenannten Inklinationswinkel von ungefähr 64°. Die horizontale Komponente ist also in Deutschland kleiner als die senkrecht in den Boden weisende, vertikale Komponente.

Mit Hilfe einer Spule und eines Kompasses kann man relativ einfach die horizontale Komponente des Erdmagnetfeldes messen. Dazu legt man die Spule in West-Ost-Richtung auf einen Tisch und stellt einen Kompass in die Spule, der sich dann nach Norden ausrichtet. Jetzt läßt man genau soviel Strom durch die Spule fließen, bis die Kompassnadel entweder nach Nord-Ost oder nach Nord-West zeigt. (Wovon hängt das ab?)

a) Die Spule ist 30cm lang und hat 100 Windungen. Bei einer Stromstärke von 48mA zeigt die Nadel genau nach Nord-Ost. Berechnen Sie daraus die Horizontalkomponente.

b) Berechnen Sie mit Hilfe des Inklinationswinkels von 64° auch die vertikale Komponente und die gesamte Feldstärke des Erdmagnetfeldes.

Messen der magnetischen Ladung

a) Beschreiben Sie ein Verfahren, mit dem man die magnetische Ladung eines Festmagneten bestimmen kann.

b) Der Nordpol eines Dauermagneten erfährt im Inneren einer Spule eine Kraft von 0,3N. Die Spule hat 500 Windungen und es fließt ein Strom der Stärke 2A hindurch. Die Länge der Spule beträgt 10cm.

b1) Wieviel magnetische Ladung "sitzt" auf dem Nordpol?

b2) Wieso ist es wichtig, dass der Südpol relativ weit entfernt ist?

b3) Was erwarten Sie, wenn man die Kraftwirkung auf den Südpol misst? (Was folgt daraus?)

Kraftwirkung auf elektrische Stöme im Magnetfeld

Zug- und Druckspannungen im Magnetfeld

Kraft zwischen (anti-)parallelen Strömen I

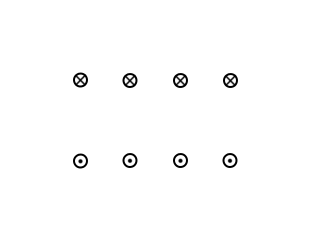
In den Zeichnungen ist ein senkrechter Schnitt durch zwei stromdurchflossene parallele Kabel dargestellt. Die Stromrichtung ist durch ein Kreuz oder einen Punkt markiert.

a) Zeichnen Sie einige Feldlinien in roter Farbe und einige Feldflächen in grüner Farbe ein.

• 
• 

b) Wie wirkt das Magnetfeld auf die Kabel? Zeichnen Sie Kraftpfeile ein.

c) Erklären Sie die Kraftwirkung mit Hilfe von Zug- und Druckspannungen.

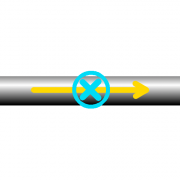
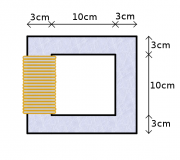
Kräfte auf Kabel und Spule

Hier ist der senkrechte Schnitt durch ein stromdurchflossenes Kabel und eine stromdurchflossene Spule dargestellt.

• 
• 

a) Zeichnen Sie einige Feldlinien (rot) und Feldflächen (grün) ein.

b) Welche Wirkung haben die Zug- und Druckspannungen auf das Kabel und welche auf die Spule?

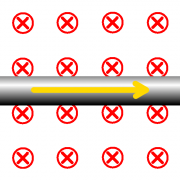
Strom verändert das homogene Feld

Ein stromdurchflossenes Kabel befindet sich zwischen den Polen eines Rechteckmagneten. Durch das Magnetfeld des Kabels verändert sich das Feld zwischen den Polen.

a) Zeichen Sie einige Feldlinien (rot) und Flächen (grün) ein.

b) Erklären Sie die Kraftwirkung mit Hilfe von Zug- und Druckspannungen.

c) Erläutern Sie die "Drei-Finger-Regel" oder auch "UVW-Regel" und kennzeichnen Sie die Richtung der Lorentzkraft mit einem Pfeil. Warum verwenden manche die linke und manche die rechte Hand?

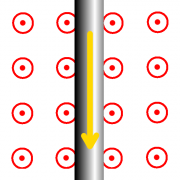
Lorentzkraft auf Probeströme im Feld

Richtung der Lorentzkraft

Ein stromdurchflossenes Kabel befindet sich in einem homogenen Magnetfeld. Die (technische) Stromrichtung ist mit einem gelben Pfeil gekennzeichnet, die Feldlinienrichtung mit einem roten und die Richtung der Kraft mit einem blauen Pfeil.

• Ergänzen Sie in den Zeichnungen die fehlende Kraft-, Strom oder Feldlinienrichtung in der entsprechenden Farbe.

• 
• 
• 
• 
• 
• 

Kraft zwischen (anti-)parallelen Strömen II

Dargestellt ist der senkrechte Schnitt durch zwei parallele Kabel und die Stromrichtungen. Die Kabel sind 3cm voneinander entfernt und einen halben Meter lang. (Die Dicke der Kabel wird vernachlässigt.) Durch das linke Kabel fließt ein Strom der Stärke von 20 Ampère, durch das rechte ein Strom der Stärke von 3 Ampère.
Um die Kraftwirkung auf das rechte Kabel zu berechnen, betrachtet man den rechten Strom als Probestrom im Feld des linken Kabels.

a) Zeichen Sie einige Feldlinien des Magnetfeldes des linken Kabels ein.

b) Bestimmen Sie mit der Drei-Finger-Regel die Richtung der Lorentzkraft auf den rechten Strom und zeichnen Sie die Kraftrichtung ein.

c) Berechnen Sie die Feldstärke des linken Magnetfeldes an der Stelle, an der sich das rechte Kabel befindet.

d) Berechnen Sie nun die Lorentzkraft auf den rechten Leiter.

e) Berechnen Sie nach der gleichen Methode die Lorentzkraft auf den linken Leiter. Überrascht Sie das Ergebnis?

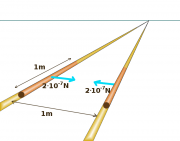
Definition des Ampères

Die Einheit der elektrischen Stromstärke, das Ampère, ist eine der sieben Basiseinheiten des internationalen Einheitensystems (SI). Alle weiteren Einheiten lassen sich auf diese sieben Basiseinheiten zurückführen. Mit Hilfe von sieben mehr oder weniger praktikablen Messvorschriften wird jeweils eine Einheit festgelegt. Die Definition des Ampères lautet (noch bis ca. 2018):

Das Ampere ist die Stärke eines konstanten elektrischen Stromes, der, durch zwei parallele, geradlinige, unendlich lange und im Vakuum im Abstand von einem Meter voneinander angeordnete Leiter von vernachlässigbar kleinem, kreisförmigem Querschnitt fließend, zwischen diesen Leitern je einem Meter Leiterlänge die Kraft [math]2 \!\cdot\! 10^{–7}[/math] Newton hervorrufen würde.

Die Festlegung des Ampères gehört offensichtlich zu den nicht praktikablen Festlegungen. Aber wieso diese scheinbar willkürliche Kraft von [math]2 \!\cdot\! 10^{–7}[/math] Newton pro Meter?

Berechnen Sie dazu die Kraft, die auf ein ein Meter langes Teilstück dieser "unendlich" langen Leiter ausgeübt wird. (Vergleiche dazu die Aufgabe "Kraft zwischen (anti-)parallelen Strömen II"!)

Feldstärkemessung mit Probestrom

Ein schon älteres Modell eines Elektromagneten mit eingezeichneten Polen, Feldlinien und Flächen.

Um die magnetische Feldstärke eines Elektromagneten zu messen, hängt man ein 2cm langes Leiterstück senkrecht zu den Feldlinien in das Magnetfeld und misst die darauf wirkende Lorentzkraft. Bei einer Stromstärke von 20A bestimmt man die Kraftwirkung zu 35mN.

Berechnen Sie die Feldstärke des Magnetfeldes.

Kabel im Erdmagnetfeld

Das Erdmagnetfeld hat in Deutschland eine Stärke von ca. 40A/m. (Das entspricht ca. 50 mikroTesla.)

a) Welche Kraft erfährt ein Stromkabel, dass von 20A durchflossen wird und 1m lang ist maximal?

b) Wie muss man das Kabel ausrichten, um die wirkende Kraft möglichst groß oder möglichst klein zu haben?

Lorentzkraft auf bewegte Ladungen im Magnetfeld

Flugbahnen

Die geladenen Teilchen bewegen sich auf ein begrenztes und homogenes Magnetfeld zu.

a) in welche Richtung wirkt beim Eintauchen in das Magnetfeld die Lorentzkraft?

b) Beschreiben Sie die Bahnkurve der Teilchen nach dem Eintauchen und skizzieren Sie eine mögliche in der Zeichnung.

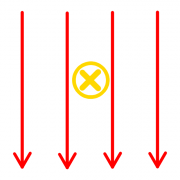
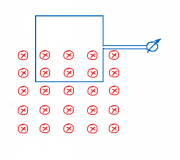
Sonnenwind trifft auf das Erdmagnetfeld

Eine künstlerische Darstellung des Erdmagnetfeldes und des Sonnenwindes.

Der sogenannte "Sonnenwind" besteht aus schnellen, elektrisch positiv oder negativ geladenen Teilchen, die von der Sonne ausgesendet werden. In der Zeichnung sind vier Teilchen und deren Bewegungsrichtung eingezeichnet.

Kennzeichnen Sie die Kraftrichtung auf die Teilchen mit einem Pfeil.

Erklären Sie wie sich die Bahn der Teilchen durch das Erdmagnetfeld ändert.

Hall-Sonde

• Erklären Sie die prinzipielle Funktionsweise einer Hall-Sonde.

• Es wird der Hall-Effekt bei einem Halbleiter und bei Silber untersucht. Folgende Messwerte wurden gefunden:

Silber: (effektive)Länge l=5mm Höhe h=2cm Dicke d=0,1mm Stromstärke I=20A, Hallspannung U= 0,01 mV

Germanium, p-dotiert: Länge l=10mm Höhe h=5mm Dicke d=1mm Stromstärke I=80mA, Hallspannung U= -40mV

In beiden Fällen betrug die magnetische Feldstärke 80000A/m.

a) Berechnen Sie jeweils die Geschwindigkeiten der Ladungsträger.

b) Warum ist das Vorzeichen der Hallspannung unterschiedlich?

Grundlagen des Induktionsgesetzes

Verschiedene Wege zur Induktionsspannung

• Zählen Sie möglichst viele verschiedene Möglichkeiten auf, wie man experimentell Induktionsspannung an einer Leiterschleife hervorrufen kann und erläutern Sie diese.

Magnetischer Fluss

• Erläutern Sie anhand von verschiedenen Beispielen, was der magnetische Fluss durch eine Fläche ist.

Induktionsgesetz

• Wie lautet das Induktionsgesetz in Worten?
• Wie lautet das Induktionsgesetz als Formel in den folgenden Situationen:
  • Allgemeingültig
  • Nur die Feldstärke ändert sich, Schleifenfläche und Magnetisierung sind konstant.
  • Nur die Schleifenfläche ändert sich, die Feldstärke und die Magnetisierung sind konstant.
  • Nur die Magnetisierung ändert sich, Schleifenfläche und Feldstärke sind konstant.

Anwendung des Induktionsgesetzes

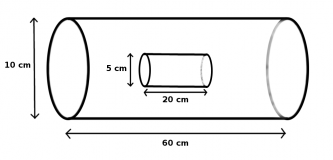
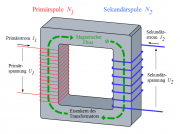
Primär und Sekundärspule

Innerhalb einer "großen" Primärspule mit 500 Windungen liegt eine "kleine" Sekundärspule mit 2000 Windungen. (Siehe Zeichnung) Durch die Primärspule fließt ein Strom von zwei Ampère.

Die Spule wird dann von der Spannungsquelle getrennt, wodurch die Stromstärke innerhalb von einer tausendstel Sekunde auf Null Ampère zurückgeht.

a) Wie groß ist zu Beginn die magnetische Feldstärke? Berechnen Sie den magnetischen Fluss durch die Primär- und die Sekundärspule.

b) Während des Trennens von der Spannungsquelle registriert die Sekundärspule eine Spannung. Begründen Sie dies und berechnen Sie die Spannung.

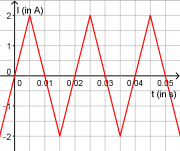
Danach legt man an die Primärspule eine Dreiecksspannung mit einer Frequenz von 50Hz an, die zu einer maximalen Stromstärke von 2A führt. (Siehe Zeichnung) Zur Messung der Spannung an der Sekundärspule wird ein Oszilloskop angeschlossen.

c) Zeichnen Sie in ein Koordinatensystem den zeitlichen Verlauf der mit dem Oszilloskop gemessenen Induktionsspannung ein.

Wie ändert sich der Verlauf der Induktionsspannung, wenn die Sekundärspule in einem Winkel von 30° in der Primärspule liegt?

Eine Spule taucht ein

Eine Spule wird innerhalb von 2 Sekunden in ein homogenes Magnetfeld mit einer Feldstärke von 1000A/m senkrecht zu den Feldlinien eingetaucht. Die Spule hat einen quadratischen Querschnitt von 5cm Kantenlänge und 300 Windungen. Sie ist an ein Spannungsmessgerät angeschlossen.

a) Berechnen Sie die gemessene Induktionsspannung.

b) Was kann man messen, wenn die Spule innerhalb des Feldes bewegt wird?

c) Kennzeichnen Sie die Polung der Induktionsspannung mit + und - in der Zeichnung.

Magnet im freien Fall

Ein Permanentmagnet wird über eine Spule gehalten und losgelassen. An die Spule ist ein Oszilloskop angeschlossen.

• Zeichnen Sie den zeitlichen Verlauf der gemessenen Induktionsspannung qualitativ in ein Koordinatensystem und erläutern Sie ihr Ergebnis.

Energieübertragung

Transformator

a) Warum kann man einen Transformator nicht mit Gleichstrom, sondern nur mit Wechselstrom betreiben?

b) Erläutern Sie anhand der Zeichnung die Funktionsweise eines Trafos.

c) Entwerfen Sie den Trafo eines Netzgerätes, der ein ein Handy mit 5,7V Spannung versorgt.

d) Ein elektrisches Schweißgerät wird an europäische Netzspannung angeschlossen. Es hat eine Primärspule mit 500 Windungen und eine Sekundärspule mit nur 5 Windungen. Der ohmsche Widerstand der Sekundärspule beträgt ca. [math]0{,}011 \,\rm \Omega[/math].

Welche Spannung liegt an der Sekundärspule an und wie groß ist dort die Stromstärke?

Welche Leistung hat das Schweißgerät?

Ein schwingender Magnet

Der Nordpol eines Stabmagneten schwingt innerhalb einer Spule auf und ab. Sobald man die Spule mit einem Kabel kurzschließt, wird der Magnet gebremst und bleibt schließlich stehen.

a) Erklären Sie diese Beobachtung.

b) Was würde passieren, wenn man den Versuch mit einer supraleitenden Spule durchführen würde?

Ein fallender Magnet

Ein Magnet fällt durch ein Kupferrohr

a) Was kann man beobachten? Wie kann man diese Beobachtung erklären?

b) Wieso kann man für den Versuch kein Plastikrohr und auch kein Eisenrohr verwenden?

c) Wie verändert sich das Versuchsergebnis, wenn man ein Kupferrohr mit dickeren Wänden benutzt?

d) Wie kann man es erreichen, dass der Magnet schwebt?

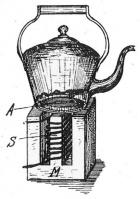
Induktionskochplatte

Eine alte Induktionskochplatte von 1909.

• Erklären Sie in Text und Bild, wie eine Induktionskochplatte funktioniert.
• Induktionsherde haben in der Regel eine hitzebeständige Glasplatte als Topfauflage. Warum erhitzt der Herd nur den Topf und nicht das darin befindliche Essen oder die Glasplatte? (Warum wird die Glasplatte beim Kochen trotzdem heiß?)

Wirbelstrombremse

• Nennen Sie Beispiele, bei denen eine Wirbelstrombremse eingesetzt wird.
• Erläutern Sie das Funktionsprinzip mit einer Zeichnung.

Erklären Sie dabei mit Hilfe des Induktionsgesetzes, wie die Ströme fließen.

• Wie kann man die Bremswirkung mit der Energieerhaltung begründen?

Spule und Magnetfeld als Energiespeicher

Selbstinduktion

a) Erklären Sie den Begriff der Selbstinduktion indem Sie einen passenden Versuch beschreiben.

b) Begründen Sie, warum die Spannung der Selbstinduktion an einer Spule proportional zur Änderung der Stromstärke ist.

Induktivität und Energiegehalt einer Spule

a) Eine Spule hat eine Induktivität von 10 H (Henry).

Was bedeutet das? Erläutern Sie es anhand von Verwendungsbeispielen.

b) Eine Spule hat 1000 Windungen, eine Querschnittsfläche von 3cm x 3cm und eine Länge von 10cm.

a) Berechnen Sie ihre Induktivität.

Man läßt einen Strom mit der Stärke von 2A durch die Spule fließen.

b) Berechnen Sie den magnetischen Fluss, die Feldstärke, die Energiemenge und die Energiedichte der Spule.

Die stromdurchflossene Spule wird nun in einen geschlossenen Eisenkern mit der relativen Permeabilität von 2000 gestellt.

c) Wie verändern sich dadurch die Werte von Frage b)?

Energie des Erdmagnetfeldes

Das Erdmagnetfeld hat in Europa eine Feldstärke von ca. 40A/m, bzw. eine Flußdichte von ca.50 MikroTesla.

Wieviel Energie ist innerhalb Ihres Zimmers im Erdmagnetfeld gespeichert?

Wie hoch könnte man damit eine Tafel Schokolade heben?

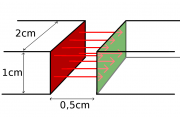
Feldenergie von Festmagneten

Zwei Festmagnete "haften" aneinander und werden bis auf einen Abstand von 0,5cm auseinandergezogen. Wieviel Energie war wohl dazu nötig?

Näherungsweise nimmt man das Feld zwischen den Polen als homogen an. Die Feldstärke zwischen den Polen wird zu 120000A/m gemessen. (Die Flußdichte beträgt 0,15T.)

supraleitender Energiespeicher

Supraleiter sind Materialien, die bei niedrigen Temperaturen keinen ohmschen Widerstand mehr haben. Daraus kann man supraleitende Kabel herstellen und auch Spulen wickeln.

a) Entwerfen Sie eine supraleitende Spule, welche die Energie eines Liters Benzin (ca. 40MJ) speichern kann.

b) Welche Vor- und Nachteile hätte die Verwendung eines Eisenkerns?

Bewegungsenergie der Elektronen

Bei einer stromdurchflossenen Spule bewegen sich die Ladungsträger, in diesem Fall also die Elektronen. In dieser Bewegung steckt auch Energie. Vielleicht ist dort auch die Energie der Spule gespeichert und nicht im Magnetfeld? Als Beispiel nehmen wir eine Spule mit 1000 Windungen, einer Querschnittsfläche von 3cm x 3cm und einer Länge von 10cm.
Zunächst muss man die Masse der im Kupferdraht frei beweglichen Elektronen berechnen. Der Draht hat eine Masse von 120g. Jedes Kupferatom stellt ungefähr ein Leitungselektron zur Verfügung. Die Dichte von Kupfer beträgt ca. 9 g/cm^3 und das molare Volumen beträgt ca. 7*10^-6 m^3/mol.

a) Wieviel Masse haben die Leitungselektronen des Kupferdrahtes?

b) Welche Geschwindigkeit müßten die Elektronen haben, um die Energie bei einer Stromstärke von 2A zu speichern?