Aufgaben zum Elektro-Magnetismus (Lösungen)

Grundlagen

Verschiedene Wege zur Induktionsspannung

Zählen Sie möglichst viele verschiedene Möglichkeiten auf, wie man experimentell Induktionsspannung an einer Leiterschleife hervorrufen kann und erläutern Sie diese.

• Eine Leiterschleife in ein Magnetfeld eintauchen (herausziehen).

Durch das Eintauchen vergrößert (verringert) sich die "Anzahl der Feldlinien" durch die Schleife, genauer nimmt der magnetische Fluss durch die Schleife zu (ab). Es wird eine Spannung an der Schleife erzeugt (andere Polung).

• Eine Leiterschleife in einem Magnetfeld vergrößern (verkleinern). Auch hier darf die Schleife dabei nicht parallel zu den Feldlinien sein.

Wiederum nimmt der magnetische Fluss durch die Schleife zu (ab).

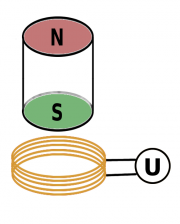
• Der Nordpol eines Festmagneten wird der Schleife genähert.

Die Feldstärke ist in der Nähe des Pols größer, deshalb nimmt der magnetische Fluß durch die Schleife zu.

• Die Schleife befindet sich im Magnetfeld einer Spule. Der Strom durch die Spule steigt an (nimmt ab).

Durch die Zunahme des Stromes steigt auch die Feldstärke innerhalb der Spule an und somit der magnetische Fluß durch die Schleife. (Bei abnehmender Stromstärke sinkt der Fluß und die Polung der Spannung ist umgekehrt.)

• Die Schleife befindet sich um einen Eisenkern. Der Pol eines Festmagneten wird dem Eisenkern genähert.

Durch die Annäherung des Magneten vergrößert sich die Magnetisierung des Eisens und der magnetische Fluss durch die Schleife nimmt zu.

• Die Schleife und eine Spule befinden sich um einen Eisenkern, sie sind "induktiv gekoppelt". Durch die Spule fließt ein Strom mit zunehmender Stromstärke.

Der Spulenstrom führt zu einer Magnetisierung des Eisenkerns. Da die Stromstärke zunimmt, steigt auch die Magnetisierung mit der Zeit an. Dadurch steigt der magnetische Fluss durch die Schleife an und eine Spannung wird erzeugt.

• Eine Schleife wird in einem Magnetfeld gedreht. Die Drehachse ist nicht parallel zu den Feldlinien.

Je nach Lage der Schleife "gehen viele oder wenige Feldlinien durch die Schleife", der magnetische Fluß ist groß oder klein. Ist die Schleife parallel zu den Feldlinien, so verschwindet der Fluß durch die Schleife. Die Drehung führt daher zu einer Änderung des magnetischen Flußes durch die Schleife und somit zu einer Induktionsspannung.

Magnetischer Fluss

Erläutern Sie anhand von verschiedenen Beispielen, was der magnetische Fluss durch eine Fläche ist.

• Hält man den Pol eines Festmagneten nahe vor eine Leiterschleife, so ist der magnetische Fluß durch die von der Schleife umrandete Fläche groß, weil "viele Magnetfeldlinien" durch die Fläche gehen. Genauer ist das Produkt von mittlerer Feldstärke und Fläche groß.
• Hält man den Festmagneten so an die Schleife, dass die Feldlinien parallel zur Schleife sind, so verlaufen gar keine Feldlinien durch die Fläche und der magnetische Fluß verschwindet. In diesem Fall ist das Produkt von Feldstärke und Fläche Null, weil die effektive Fläche senkrecht zu den Feldlinien Null ist.
• Befindet sich ein magnetisierter Eisenkern in einer Leiterschleife, so gibt es einen magnetischen Fluß durch die Fläche der Schleife, weil "viele Magnetisierungslinien" durch die Fläche gehen. Genauer ist der magnetische Fluß das Produkt aus mittlerer Magnetisierung und Fläche.

Induktionsgesetz

• Wie lautet das Induktionsgesetz in Worten?
• Wie lautet das Induktionsgesetz als Formel in den folgenden Situationen:
  • Allgemeingültig
  • Nur die Feldstärke ändert sich, Schleifenfläche und Magnetisierung sind konstant.
  • Nur die Schleifenfläche ändert sich, die Feldstärke und die Magnetisierung sind konstant.
  • Nur die Magnetisierung ändert sich, Schleifenfläche und Feldstärke sind konstant.

Anwendung des Induktionsgesetzes

Primär und Sekundärspule

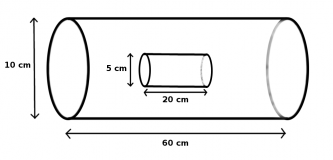
Innerhalb einer "großen" Primärspule mit 500 Windungen liegt eine "kleine" Sekundärspule mit 2000 Windungen. (Siehe Zeichnung) Durch die Primärspule fließt ein Strom von zwei Ampère.

Die Spule wird dann von der Spannungsquelle getrennt, wodurch die Stromstärke innerhalb von einer tausendstel Sekunde auf Null Ampère zurückgeht.

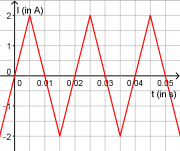
Danach legt man an die Primärspule eine Dreiecksspannung mit einer Frequenz von 50Hz an, die zu einer maximalen Stromstärke von 2A führt. (Siehe Zeichnung) Zur Messung der Spannung an der Sekundärspule wird ein Oszilloskop angeschlossen.

a) Wie groß ist zu Beginn die magnetische Feldstärke? Berechnen Sie den magnetischen Fluß durch die Primär- und die Sekundärspule.

Die Spule betrachtet man als "schlanke Spule" und berechnet dann nach der Definition der magnetischen Feldstärke:

[math]H=\frac{n_1\, I}{l}= \rm \frac{500\cdot 2\,A}{0{,}6\,m}= \rm 1667\, \frac{A}{m}[/math]

Die Luft ist nicht magnetisierbar, deswegen ist die Flußdichte einfach das Produkt der Feldstärke mit der Feldkonstante:

[math]B=\mu_0\,H = 1{,}2566\cdot 10^{-6} \frac{\rm V\, s}{\rm A\,m} \cdot 1667\, \rm \frac{A}{m}= 0{,}002095\,T \quad (= 2{,}095\,mT)[/math]

Die Fläche der Spulen berechnet sich mit Hilfe des Radius:

[math]A_1=\pi\, r_1^2 = \pi\cdot (0{,}05\,\rm m)^2 = 0{,}007854\,\rm m^2 \quad (= 78{,}54\,\rm cm^2)[/math]

[math]A_2=\pi\, r_2^2 = \pi\cdot (0{,}025\,\rm m)^2 = 0{,}001969\,\rm m^2 \quad (= 19{,}69\,\rm cm^2)[/math]

Aus der Flußdichte und der Fläche kann man nun den magnetischen Fluß berechnen:

[math]\Phi_1 = B\, A_1 = 2{,}095\,\rm mT \cdot 0{,}007854\,\rm m^2 = 1{,}645\cdot 10^{-5}\,\rm T m^2 \quad (V \cdot s\,\text{oder}\,Wb)[/math]

[math]\Phi_2 = B\, A_2 = 2{,}095\,\rm mT \cdot 0{,}001969\,\rm m^2 = 4{,}114\cdot 10^{-6}\,\rm T m^2 [/math]

b) Während des Trennens von der Spannungsquelle registriert die Sekundärspule eine Spannung. Begründen Sie dies und berechnen Sie die Spannung.

Durch die fehlende Spannung sinkt die Stromstärke auf Null ab. Währenddessen ändert sich die Feldstärke und damit auch der magnetische Fluß in der Sekundärspule.

Zur Berechnung der Induktionsspannung verwendet man das Induktionsgesetz:

[math]U_i = n_2\,\dot \Phi = n_2\,\frac{\Delta \Phi}{\Delta t} =2000\cdot \frac{4{,}114\cdot 10^{-6}\,\rm T m^2}{10^{-3}\,\rm s} = 8{,}23\,\rm V \qquad \left({\rm\frac{\frac{V \, s}{m^2}}{s}} = V \right)[/math]

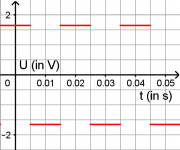
c) Zeichnen Sie in ein Koordinatensystem den zeitlichen Verlauf der mit dem Oszilloskop gemessenen Induktionsspannung ein.

Wieder wird durch die Änderung der Stromstärke der magnetische Fluß geändert.Im Induktionsgesetz kann man sich nun aussuchen, welche Änderungsrate man ausrechnet. Man kann die Änderung der Flußdichte, der Feldstärke oder der Stromstärke verwenden:

[math]U_i = n_2\,\dot \Phi = n_2 \,\dot B\, A = n_2 \,\mu_0 \dot H \, A = n_2 \,\mu_0 \frac{n_1}{l} \dot I \, A \qquad \left(= \mu_0 \, \frac{A\, n_1\, n_2}{l} \cdot \dot I \right)[/math]

Weil hier die Stromstärke sich konstant ändert, kann man die Änderungsraten als Differenzenquotient berechnen:

[math]U_i = n_2 \,\frac{\Delta \Phi}{\Delta t} = n_2 \,\frac{\Delta B}{\Delta t}\, A = n_2 \,\mu_0\frac{\Delta H}{\Delta t}\, A = n_2 \,\mu_0 \frac{n_1}{l}\frac{\Delta I}{\Delta t}\, A[/math]

Die Stromstärke fällt oder oder steigt innerhalb von [math]0{,}01\,\rm s[/math] um [math]4\,\rm A[/math]:

[math]\frac{\Delta I}{\Delta t} = \rm \frac{4\,A}{0{,}01\,\rm s} = 400\,\rm\frac{A}{s}[/math]

Bei ansteigender Stromstärke beträgt die Induktionsspannung daher:

[math]U_i = n_2\,\mu_0 \frac{n_1}{l}\frac{\Delta I}{\Delta t}\, A = 2000\cdot 1{,}2566\cdot 10^{-6} \frac{\rm V\, s}{\rm A\,m} \cdot \frac{500}{0{,}6\,\rm m}\cdot \frac{4\,\rm A}{0{,}01\,\rm s}\, 0{,}001969\,\rm m^2 = 0{,}165\,\rm V \quad (= 165\,\rm mV)[/math]

Jetzt kann man den Verlauf der Induktionsspannung zeichnen:

test

Wie ändert sich der Verlauf der Induktionsspannung, wenn die Sekundärspule in einem Winkel von 45° in der Primärspule liegt?

[math][/math]

Eine Spule taucht ein

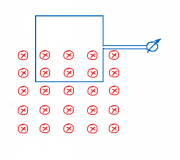
Eine Spule wird innerhalb von 2 Sekunden in ein homogenes Magnetfeld mit einer Feldstärke von 1000A/m senkrecht zu den Feldlinien eingetaucht. Die Spule hat einen quadratischen Querschnitt von 5cm Kantenlänge und 300 Windungen. Sie ist an ein Spannungsmessgerät angeschlossen.

a) Berechnen Sie die gemessene Induktionsspannung.

b) Was kann man messen, wenn die Spule innerhalb des Feldes bewegt wird?

c) Kennzeichnen Sie die Polung der Induktionsspannung mit + und - in der Zeichnung.

Magnet im freien Fall

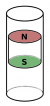
Ein Permanentmagnet wird über eine Spule gehalten und losgelassen. An die Spule ist ein Oszilloskop angeschlossen.

• Zeichnen Sie den zeitlichen Verlauf der gemessenen Induktionsspannung qualitativ in ein Koordinatensystem und erläutern Sie ihr Ergebnis.

Energieübertragung

Transformator

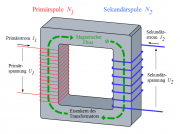
a) Warum kann man einen Transformator nicht mit Gleichstrom, sondern nur mit Wechselstrom betreiben?

b) Erläutern Sie anhand der Zeichnung die Funktionsweise eines Trafos.

c) Wie könnte der Trafo eines Netzgerätes gebaut sein, der ein Handy mit 5,7V Spannung versorgt?

Ein schwingender Magnet

Der Nordpol eines Stabmagneten schwingt innerhalb einer Spule auf und ab. Sobald man die Spule mit einem Kabel kurzschließt, wird der Magnet gebremst und bleibt schließlich stehen.

a) Erklären Sie diese Beobachtung.

b) Was würde passieren, wenn man den Versuch mit einer supraleitenden Spule durchführen würde?

Ein fallender Magnet

Ein Magnet fällt durch ein Kupferrohr

a) Was kann man beobachten?

b) Wieso kann man für den Versuch kein Plastikrohr und auch kein Eisenrohr verwenden?

c) Wie verändert sich das Versuchsergebnis, wenn man ein Kupferrohr mit dickeren Wänden benutzt?

d) Wie könnte man es erreichen, dass der Magnet schwebt?

Wirbelstrombremse

• Nennen Sie Beispiele, bei denen eine Wirbelstrombremse eingesetzt wird.
• Erläutern Sie das Funktionsprinzip mit einer Zeichnung.

Erklären Sie dabei mit Hilfe des Induktionsgesetzes, wie die Ströme fließen.

• Wie kann man die Bremswirkung mit der Energieerhaltung begründen?

Selbstinduktion

a) Erklären Sie den Begriff der Selbstinduktion indem Sie einen passenden Versuch beschreiben.

b) Begründen Sie, warum die Spannung der Selbstinduktion an einer Spule proportional zur Änderung der Stromstärke ist.

Induktivität

a) Eine Spule hat eine Induktivität von 10 H (Henry).

Was bedeutet das?

b) Eine Spule hat 1000 Windungen und einen geschlossenen Eisenkern mit einer Permeabilitätszahl von [math]\mu_r = 2000[/math].

Berechnen Sie ihre Induktivität.