Aufgaben zu Wellen

(Kursstufe > Mechanische Wellen)

Aufgaben

Grundlagen

1) Nennen Sie die typischen Eigenschaften einer Welle.

2) Erklären Sie die folgenden Begriffe anhand einer La Ola Welle in einem Stadion:

• Transversal/Longitudinalwelle
• Phasengeschwindigkeit
• Wellenzug/homogene Welle
• Amplitude
• Frequenz
• Wellenlänge

3) Geben Sie Beispiele für Longitudinal- und Transversalwellen an und erklären Sie den Unterschied.

4) Machen Sie anhand der La Ola Welle in einem Stadion klar, dass die Ausbreitungsgeschwindigkeit von der Kopplungsstärke der Schwinger, aber nicht von der Frequenz oder der Amplitude abhängt.

5) Erläutern Sie warum Longitudinalwellen in der Regel schneller sind als Transversalwellen.

7) Bei Erdbeben werden zunächst sogenannte "Primärwellen" (P-Wellen) registriert, einige Sekunden später die "Sekundärwellen" (S-Wellen). Erklären Sie dieses Phänomen physikalisch.

8) Geben Sie je ein Beispiel für eine Kugel- und eine Kreiswelle an.

9) a) Erklären Sie warum bei einer Kugelwelle die Intensität proportional zum Quadrat des Abstands abnimmt und bei einer Kreiswelle nur proportional zum Abstand.

b) Ein Lautsprecher sendet eine kugelförmige Schallwelle mit einer Leistung von drei Watt aus. Berechnen Sie die Intensität in einem Abstand von einem und von zwei Metern.

10) Geben Sie Beispiele für Wellen an, die näherungsweise Zylinder- oder ebene Wellen sind. (Wieso nur näherungsweise?)

11) Erläutern Sie die Unterschiede von Oberflächenwellen und Schwerewellen bei Wasserwellen.

12) Geben Sie den mathematischen Zusammenhang zwischen Erregerfrequenz, Phasengeschwindigkeit und Wellenlänge an.

13) a) Berechnen Sie die Wellenlängen der Schallwellen innerhalb des menschlichen Hörbereichs von 20Hz bis 20000Hz. (Recherchieren Sie die Schallgeschwindigkeit in Luft!)

b) Beschreiben Sie wie sich die Wellenlängen dieser Schallwellen im Wasser verändern. (Schallgeschwindigkeit ca. 1500 m/s)

Zeigermodell / Wellengleichung

1) Nachdem eine Schwingung innerhalb von 3 Sekunden 6 ganze Schwingungen ausgeführt hat, hat sich diese Störung um 1,8 m ausgebreitet.

a) Bestimmen Sie Frequenz, Wellenlänge und Ausbreitungsgeschwindigkeit der Welle.

b) Wie groß ist der Phasenunterschied zweier Schwingungen im Abstand von 30m?

2) Bei einer Pendelkette sind mehrere Pendel in einem Abstand von 10 cm miteinander gekoppelt.

Wird ein Pendel angeregt, so folgen die Nachbarn 0,5 s später mit einer Phasenverschiebung von [math]\pi / 16[/math]. Bestimmen Sie die Ausbreitungsgeschwindigkeit, Wellenlänge und Frequenz der Welle.

3) Stellen Sie die Wellengleichung von Aufgabe 1) und 2) auf.

4) Eine Transversalwelle hat die Wellengleichung [math]y(x,t)= 2\,{\rm cm} \, \sin(\frac{\pi}{\rm s} \cdot t -\frac{\tfrac{1}{2}\pi}{\rm cm} \cdot x)[/math].

a) Bestimmen Sie Amplitude, Periodendauer, Frequenz und Wellenlänge.

b) Zeichnen Sie die Welle zum Zeitpunkt t=0, also zu Beginn der Zeitrechnung, und 0,5 Sekunden später in ein Koordinatensystem.

5) Ein gespanntes Seil dient als Wellenträger. Das linke Ende wird mit dem Beginn der Messung sinusförmig bewegt mit einer Periodendauer von 0,8s und einer Amplitude von 20cm. Zu Beginn der Zeitmessung befindet sich der Seilanfang gerade in der Ruhelage auf dem Weg nach Oben. Vor dem Beginn der Messung ist das Seil nicht ausgelenkt.
Die Seilwelle breitet sich mit 0,6m/s aus.

a) Zeichne den Zeiger des Seilanfangs nach 1,7s und gib an wo der Seilanfang befindet und mit welcher Geschwindigkeit sich der Seilanfang bewegt.

b) Zeichne den Zustand des Seils nach 1,7s. (Maßstab: [math]10\,\rm cm \, \hat = \, 1\,\rm m[/math]

c) Zeichne ein Diagramm der Auslenkung über die Zeit für die Stelle des Seils, dass 0,55m vom Seilanfang entfernt ist.

Interferenz

Zwei Lautsprecher

• 1) Woran kann man im Alltag erkennen, dass sich Wellen störungsfrei überlagern?

• 2) Beschreiben Sie den Versuch mit den zwei Lautsprechern, die an einem Sinusgenerator angeschlossen sind.

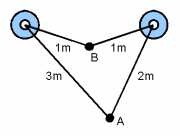
• 3) Die beiden Lautsprecher sind 1,5 m voneinander entfernt und schwingen in Phase mit einer Frequenz von 858 Hz.

a) Bestimmen Sie die Lautstärke an den Punkten A und B mit Hilfe eines Zeigerdiagramms. Vernachlässigen Sie dabei die Abnahme der Schallintensität durch den größeren Abstand vom Lautsprecher und der Dämpfung.

b) Suchen Sie zwei Stellen zwischen den Lautsprechern, bei denen der Ton besonders leise bzw. besonders laut ist.

c) Wie verändert sich qualitativ die Situation in den Punkten A und B, wenn man die Änderung der Schallintensität nicht vernachlässigt?

d) Bestimmen Sie die exakte Schwingungsgleichung für die Punkte A und B, wenn beide Lautsprecher mit einem Watt senden.

• 4) Auf der Wasseroberfläche in einem See werden mit den Füßen im Abstand von 80cm zwei Kreiswellen erzeugt. Die Füße bewegen sich gleichmäßig und in Phase auf und ab, und zwar 10 mal in 16 Sekunden. (Video von 1:30 bis 2:15) Die Ausbreitungsgeschwindigkeit der Wellen misst man zu 20cm/s.

a) Welche Wellenlänge haben die beiden Wellen?

b) Wo zwischen den Füßen befinden sich Stellen mit konstruktiver, bzw. destruktiver Interferenz? Machen Sie eine Zeichnung.

• 5) Zwei Lautsprecher erzeugen beide in einem Abstand von 1m einen Ton mit der Frequenz von 1000Hz. Zwischen den Lautsprechern misst man die Orte, an denen der Ton leise und an denen der Ton laut ist:

Bestimmen Sie aus dem Messergebnis die Schallgeschwindigkeit.

Beugung

Blick auf einen kleinen Hafen

• 1) Erklären Sie an einem Alltagsphänomen die Beugung von Wellen.
• 2) Warum haben Stereoanlagen zwei Boxen aber nur einen "Subwoofer", den man auch unter das Sofa stellen kann, was man aber besser mit den Boxen nicht tut?
• 3) Hinter einer Lärmschutzwand ist der Verkehrslärm auch ohne Sichtkontakt zur Strasse noch zu hören. Der Verkehr klingt dumpfer als beim direkten Hinhören. Erklären Sie die Beobachtungen.
• 4) Erklären Sie das Foto der Wellen an einem Hafen.

Brechung

Eine Wasserwelle läuft auf den flachen Strand zu.

1) Beschreiben Sie ein Alltagsphänomen, bei dem Brechung auftritt.

2) Erklären Sie das Phänomen der Brechung mit Hilfe des Huygenschen Prinzips.

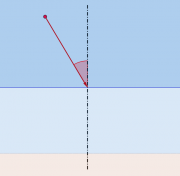
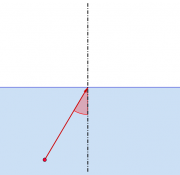
3) Eine Wasserwelle läuft im Meer quer auf das Ufer zu. Durch die geringere Wassertiefe verringert sich auch die Ausbreitungsgeschwindigkeit von 2 m/s auf nur noch 1 m/s. Vereinfachend nehmen wir zunächst an, dass der Übergang an einer Kante erfolgt.

Konstruieren Sie mit Hilfe des Huygensschen Prinzips den Verlauf der Wellenstrahlen für die Einfallswinkel 30° und 60°.

In der Realität nimmt die Wassertiefe kontinuierlich ab. Zeichnen Sie den ungefähren Verlauf der Wellenstrahlen bei einem Einfallswinkel von 60°.

Licht trifft auf die Grenze zwischen Wasser und Luft.

4) Licht hat in unterschiedlichen Medien unterschiedliche Ausbreitungsgeschwindigkeiten:

Medium	Lichtgeschwindigkeit
Luft	[math]300000\,\rm \frac{km}{s}[/math]
Wasser	[math]226000\,\rm \frac{km}{s}[/math]
Glas	[math]200000\,\rm \frac{km}{s}[/math]

a) Konstruieren Sie den Lichtweg für den Übergang zwischen Wasser und Luft für einen Einfallswinkel von 45°.

b) Was ändert sich, wenn man statt dem Übergang Wasser - Luft den Übergang Glas - Luft betrachtet? Konstruieren Sie wieder den Lichtweg für den Einfallswinkel von 45°.

5) Beschreiben Sie ein Phänomen, bei dem Totalreflektion auftritt.

6) Warum kann es beim Übergang von Luft zu Wasser für Licht keine Totalreflektion geben?

7) Leiten Sie das Brechungsgesetz her.

8) Berechnen Sie den Grenzwinkel der Totalreflektion für den Übergang von Glas zu Luft.

Reflektion

• 1) Wie wird ein Wellenberg am festen und wie am losen Ende reflektiert? Geben Sie jeweils ein reales Beispiel für eine solche Situation an.

Stehende Wellen

1) Erklären Sie mit Hilfe einer Zeichnung und eines Textes, warum die Klangstäbe des Xylophons so befestigt sind wie auf dem Bild zu sehen.

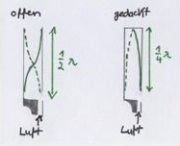
2) Bestimmen Sie die Höhe des Grundtones und des ersten Obertones der Orgelpfeife im offenen und gedackten Fall, wenn die Pfeife einen halben Meter lang ist.

Die Pfeife im Querschnitt

3) Aus dem Baden-Württembergischen Physik-Abitur 2004: Aufgabe I b).

4) Ein Aluminiumrohr wird nach ca. 1/4 der Länge mit den Fingern gehalten und mit einem Klöppel am Ende angeschlagen.

a) quer zum Rohr

b) längs zum Rohr

Messen Sie mit Hilfe einer geeigneten App die Frequenz des Tones und bestimmen Sie daraus die Phasengeschwindigkeit von Transversal- und Longitudinalwellen in dem Aluminiumrohr.