Energie und Impuls (Potential und Kraftverlauf) einer mechanischen Schwingung

Die Wege von Impuls und Energie

Ein Körper kann nie alleine schwingen. Er braucht einen Partner.
Selbst bei einem Federpendel, das z.B. an einer Wand befestigt ist (bei dem es folglich so aussieht, als würde nur ein Körper schwingen), schwingt immer ein anderer Körper, in diesem Fall die Erde, mit.

Die zwei Körper schwingen dabei um den gemeinsamen Schwerpunkt.
Bei dem oben genannten Beispiel wäre der, da die Erde ja eine viel größere Masse hat als der Rest des Federpendel, nahezu direkt an der Wand, wodurch es dem Betrachter so erscheinen kann, als würde nur das Federpendel schwingen.

Zwei Körper schwingen

Ein Vergleich der Darstellungen mit Kräften und mit dem Impulsfluss bei einer Feder unter Zugspannung.

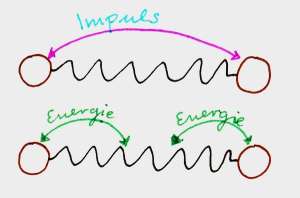
Während einer Schwingung fließt die Energie doppelt so schnell zwischen den Körpern (Bewegungsenergie) und der Feder (potentielle Energie) hin und her, wie der Impuls zwischen den zwei Körpern.

Der Impuls- und Energiefluss.

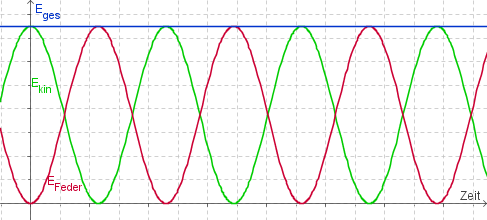
Dies lässt sich gut an dem folgenden Bild verdeutlichen.

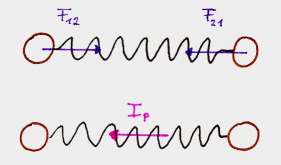
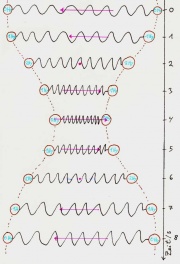
Wenn die Feder vollstängig auseinandergezogen oder zusammengedrückt ist, enthält sie alle Energie des Systems (Beide Körper bewegen sich an genau diesem Punkt nicht). Ist sie entspannt, so enthält sie gar keine. Beim folgenden Bild wäre die Energie also im ersten Abschnitt in der Feder, im dritten vollständig in den Körpern, im fünften wieder in der Feder, im siebten in den Körpern un im letzten wieder in der Feder. Sie hat sich also zwei mal zwischen Feder und den Körpern hin und her bewegt.

Der Impuls wandert hingegen nur einmal zwischen den Körpern hin und her:
Im ersten Abschnitt haben beide Körper keinen Impuls, im dritten hat der linke Körper den maximalen Impuls, während der rechte den maximalen negativen Impuls hat, im fünften haben beide wieder gar keinen, im siebten hat der rechte den positiven und der linke den negativen Impuls und am Ende haben beide wieder gar keinen.

Der Impulsfluss während einer Schwingung.

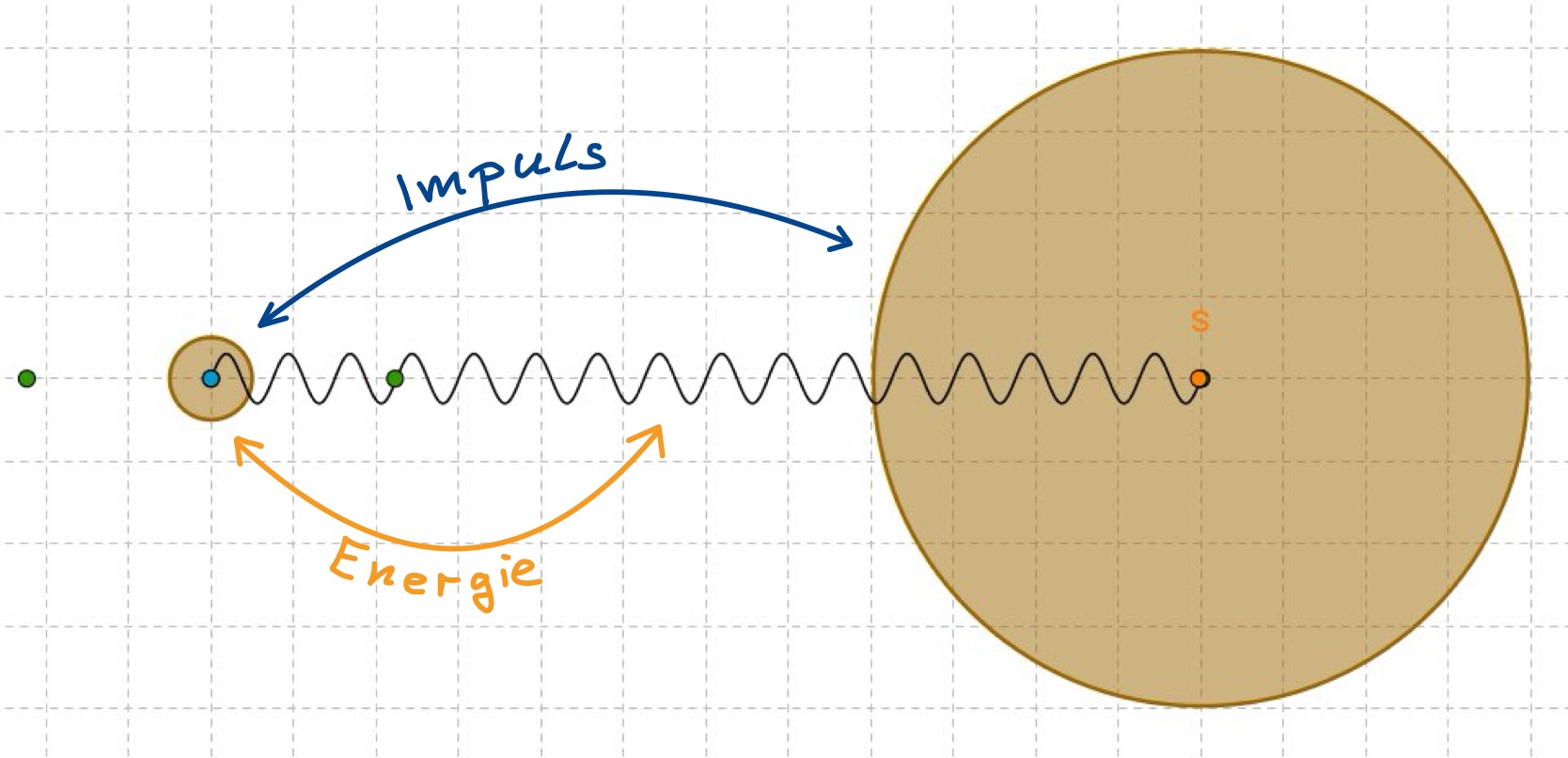
Die Erde als Schwingungspartner

Ist die Erde (oder ein ähnlich großer Körper) einer der zwei schwingenden Körper und der andere Körper ist erheblich kleiner, so nimmt die Erde zwar Impuls auf, aber kaum Energie.

Die Erde als Schwingungspartner.

Rechnung:

[math]E_{Erde}={1 \over 2} MV^2 = {P^2 \over 2M}[/math][math] \mid [/math]da [math] V = {P \over M} [/math]

[math]E_m={1 \over 2} mv^2 = {p^2 \over 2m}[/math][math] \mid [/math]da [math] v = {p \over m} [/math]

da [math] P=p[/math]

[math]\Rightarrow E_{Erde}\lt\ltE_m[/math]

Grafische Darstellungen

in Abhängigkeit von der Zeit

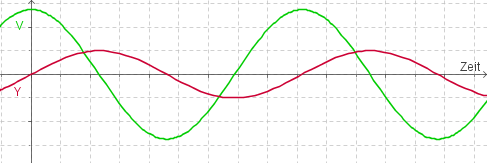
Die Geschwindigkeit und die Elongation hängen über die kinetische Energie miteinander zusammen.

Die Elongation Y und die Geschwindigkeit V in Abhängigkeit der Zeit.

Die Energie der Feder E_Feder, die Bewegungsenergie des schwingenden Körpers E_kin und die Gesamtenergie E_ges in Abhängigkeit der Zeit.

Die Gesamtenergie lässt sich auf zweit Arten bestimmen:

Über die kinetische Energie:

[math] E = {1 \over 2}mv^2[/math]
mit [math]v=\hat v = \hat y \omega[/math]

 [math]\Rightarrow E ={m \over 2}\omega^2 \hat y^2[/math]

Über die Spannenergie:

[math] E = {1 \over 2}Ds^2[/math]
mit [math]s = \hat y \omega[/math]

 [math]\Rightarrow E ={D \over 2} \hat y^2[/math]

Beide Formeln sind gleichwertig.

Die Gesamtenergie ist konstant.

in Abhängigkeit vom Ort

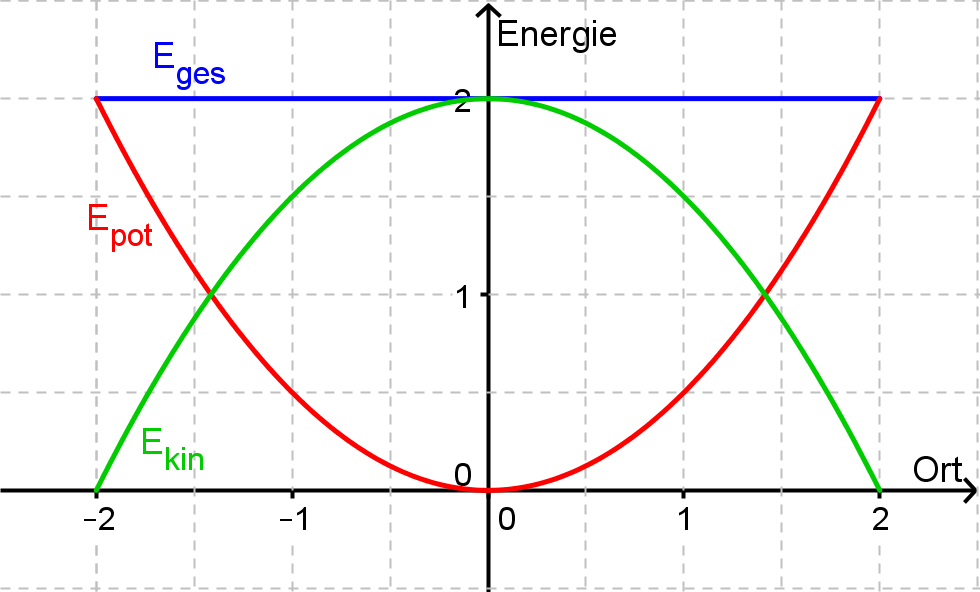
In Abhängigkeit von der Elongation steigt die potentielle Energie parabelförmig, während die kinetische Energie parabelförmig fällt.

Die Gesamtenergie ist die Addition beider Energien, bleibt also konstant.

Die Energieformen eines (horizontalen) Federpendels in Abhängigkeit vom Ort.

Formeln

Energie:

In Abhängigkeit von der Frequenz und der Amplitude: (E prop f^2 und y^2)

In Abhängigkeit von der Federstärke und der Amplitude: (E prop D und y^2)

Impuls: Ist nicht konstant!

Aufgaben

1 Schwebung

Zwei Stimmgabeln erzeugen eine Schwebung, weil die eine mit einem Reiter versehen wurde. Die Frequenz derjenigen ohne Reiter beträgt 440 Hz. Schätzen Sie die Frequenz der anderen Stimmgabel ab.

2 Überlagerung

Bestimmen Sie jeweils die Schwingung, die aus der Überlagerung von y₁ und y₂ entsteht mit Hilfe des Zeigerdiagramms:

1. [math]y_1 = 2cm \, sin(2t)\qquad y_2 = 4cm sin(2t+\pi)[/math]
2. [math]y_1 = 2cm \, sin(2t)\qquad y_2 = 4cm sin(2t+\pi/2)[/math]
3. [math]y_1 = 2cm \, sin(2t)\qquad y_2 = 2cm sin(2t+\pi)[/math]

3 Energie

Welche Energie hat eine schwingender Körper der Masse 1kg, wenn er eine Periodendauer von 1s und eine Amplitude von 1cm hat?

4 Energie

Wie muss ein Körper der Masse 1kg schwingen, damit die Schwingung 1J Energie hat?

5 Energie(y,D,m)

Wie verändert sich die in einer Federschwingung enthaltene Energiemenge, wenn

1. man die Amplitude verdoppelt?
2. man die Federhärte verdoppelt?
3. man die Masse verdoppelt?

und dabei jeweils die anderen Größen konstant hält.

6 Energie(f)

Zwei gleichschwere Körper schwingen mit der gleichen Amplitude, aber der eine doppelt so schnell wie der andere. Vergleichen sie die Energiemengen.

7 Schwingung bei bekannter Energie

Zwei Wagen, die beide eine Masse von 600g haben, sind mit einer Feder der Härte 1N/cm verbunden. Wie schwingen die Wagen, wenn ihnen eine Energie von 1Joule zugeführt wird?

8 Wasserstoffmolekül

Ein H₂-Molekül kann man idealisiert als zwei, mit einer Feder verbundene, Körper auffassen. Durch eine Messung regt man das Molekül zum Schwingen an und bestimmt die Frequenz der Schwingung zu 9,2 10¹¹ Hz.

Bestimmen sie die "Federkonstante" der gedachten Feder zwischen den Molekülen. Wieviel Energie steckt im Molekül, wenn beide Atome mit einer Amplitude von 10^-10m schwingen?

(Fehlende Angaben entnehmen sie dem Buch oder dem www.)

9 E_kin = E_Spann

Für welche Auslenkung verteilt sich die Energie eines (horizontalen) Federpendels gerade je zur Hälfte auf die Feder und den Impuls?

10 Zeitlicher Mittelwert von E_kin und E_Spann

Bestimmen sie das zeitliche Mittel der kinetischen und potentiellen Energie (Spannenergie der Feder) eines (horizontalen) Federpendels an einem selbst gewählten Beispiel. Hinweise:

[math]E_{kin}(t)=m/2 \, v(t)^2 \qquad E_{pot}=D/2 \, y(t)^2[/math]

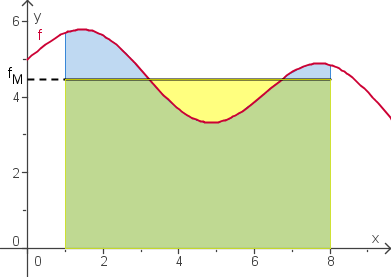
Den Mittelwert einer Funktion f(x) von x₁ bis x₂ bestimmt man mit Hilfe des Integrals:

[math]\bar f = \frac{1}{x_2 - x_1} \int_{x_1}^{x_2}f(x) dx[/math]

Anschaulich bestimmt man zur Fläche zwischen Schaubild und x-Achse ein Rechteck gleicher Fläche. Die Höhe des Rechtecks ist gerade der Mittelwert.