Beschreibung einer harmonischen Schwingung mit der Zeigerdarstellung: Unterschied zwischen den Versionen

Aus Schulphysikwiki
Wechseln zu: Navigation, Suche
(→‎Frequenz)
(→‎Animation)
 
(38 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
([[Inhalt_Kursstufe|'''Kursstufe''']] > [[Inhalt_Kursstufe#Mechanische Schwingungen|''' Mechanische Schwingungen''']])
 +
 +
 
Ausgehend von experimentellen Beobachtungen stellt man ein mathematisches Modell auf, mit dem man die Bewegung einer Schwingung beschreiben kann. Ob dieses sogenannte Zeigermodell für eine Schwingung zutrifft, kann man wiederum nur experimentell untersuchen.
 
Ausgehend von experimentellen Beobachtungen stellt man ein mathematisches Modell auf, mit dem man die Bewegung einer Schwingung beschreiben kann. Ob dieses sogenannte Zeigermodell für eine Schwingung zutrifft, kann man wiederum nur experimentell untersuchen.
  
 
Das Vorgehen ist also deduktiv, ein Modell wird im Experiment überprüft.
 
Das Vorgehen ist also deduktiv, ein Modell wird im Experiment überprüft.
  
−
Alle Schwingungen, die sich mit dem Zeigermodell beschreiben lassen, heißen harmonische Schwingungen.
+
Alle Schwingungen, die sich mit dem Zeigermodell beschreiben lassen, heißen [[Woran man eine harmonische Schwingung erkennt (Vier gleichwertige Kriterien)|harmonische Schwingungen]].
  
  
 
==Versuch: Ein Sandpendel==
 
==Versuch: Ein Sandpendel==
−
===Aufbau:===
+
;Aufbau:
−
[[Datei:Versuchsaufbau_Sandpendel.jpg|thumb|none|Versuchsaufbau des Sandpendels (1)]]
+
[[Datei:Versuchsaufbau_Sandpendel.jpg|hochkant|thumb|Versuchsaufbau des Sandpendels (1)]]
−
 
+
Ein Trichter wird mit Sand gefüllt und in Schwingungen versetzt. Unter dem Trichter befindet sich eine Tapete, die dann quer zur Schwingungsrichtung unter dem Pendel weggezogen wird.
−
Siehe Bild 1
+
<br style="clear: both" />
−
 
+
−
===Beobachtung:===
+
−
[[Datei:Versuchsergebnis_Sandpendel.jpg|thumb|none|Versuchsergebnis des Sandpendels(2)]]
+
  
 +
;Beobachtung:
 +
[[Datei:Versuchsergebnis_Sandpendel.jpg|thumb|Versuchsergebnis des Sandpendels(2)]]
 
Es entsteht eine Wellenlinie. (Siehe Bild 2)
 
Es entsteht eine Wellenlinie. (Siehe Bild 2)
  
−
===Erklärung===
+
;Erklärung
−
 
+
 
Diese Wellenlinie ist gerade das Zeit-Ort Diagramm einer Schwingung, denn sie gibt an wann der Körper wo ist. Die Ortsfunktion scheint eine Sinusfunktion zu sein, an der man die Amplitude und die Periode ablesen kann.
 
Diese Wellenlinie ist gerade das Zeit-Ort Diagramm einer Schwingung, denn sie gibt an wann der Körper wo ist. Die Ortsfunktion scheint eine Sinusfunktion zu sein, an der man die Amplitude und die Periode ablesen kann.
  
 
==Versuch: Projektion der Kreisbewegung==
 
==Versuch: Projektion der Kreisbewegung==
−
===Aufbau:===
+
;Aufbau:
−
[[Datei:Versuchsaufbau_Projektion_der_Kreisbewegung.jpg|thumb|none|Versuchsaufbau Projektion der Kreisbewegung(3)]]
+
  
 +
<gallery widths=150px heights=130px >
 +
Bild:Versuchsaufbau_Projektion_der_Kreisbewegung.jpg|Versuchsaufbau mit einem Zeunerwagen und einer Glühlampe
 +
Bild:Schwingung_Zeiger_Versuchsaufbau.jpg|oder so...
 +
Bild:Schwingung Zeiger Versuchsaufbau Federpendel vertikal.jpg|Das vertikale Federpendel
 +
Bild:Schwingung_Zeiger_Versuchsaufbau_Wagen.jpg|und das horizontale Federpendel.
 +
Bild:|
 +
</gallery>
  
−
Variation der Drehgeschwindigkeit oder Variation der Schwingung durch Veränderung der Masse und Feder. Die Veränderung der Schwingung ist exakter durchführbar!
+
Direkt neben den schwingenden Wagen oder das schwingende Männchen wird ein Motor mit einem exzentrischen Stift befestigt.  
  
−
===Beobachtung:===
+
Eine Lampe oder ein Diaprojektor wirft von beiden einen Schatten an die Wand.
  
−
Text Text Text Text Text Text TextText Text Text Text Text Text Text Text Text Text Text
+
Man versucht nun zu erreichen, dass der Schatten des Wagens (oder des Männchens) sich genauso wie der Schatten des sich drehenden Stiftes bewegt. Zunächst stellt man dazu die Drehgeschwindigkeit des Motors in etwa ein. Die Frequenz des Federpendels ist aber exakter regulierbar, indem man z.B. mit Knete die Masse vergrößert.
  
−
===Erklärung===
+
;Beobachtung:
 +
Wenn die Umlaufzeit genau mit der Periodendauer der Schwingung übereinstimmt und
 +
die Amplitude der Schwingung genausogroß ist wie der Stift von der Mitte entfernt ist und
 +
man im richtigen Moment losläßt,
 +
dann bewegen sich die Schatten ganz gleich auf der Wand hin und her.
  
−
Text Text Text Text Text Text TextText Text Text Text Text Text Text Text Text Text Text
+
[[Media:Schwingung_Zeiger_Seite.ogg|Video]] von der Seite.
 +
[[Media:Schwingung_Zeiger_Projektion_Schatten.ogg|Video]] der Schattenprojektion.
 +
 
 +
;Folgerung
 +
Man kann den Ort eines harmonischen Schwingers durch die Projektion einer Kreisbewegung beschreiben!
  
 
==Die Zeigerdarstellung==
 
==Die Zeigerdarstellung==
Zeile 43: Zeile 58:
 
* Die Länge des Zeigers entspricht der Amplitude der Schwingung. (Nur bei einer idealisierten ungedämpften Schwingung ohne Reibung ist also die Zeigerlänge konstant.)  
 
* Die Länge des Zeigers entspricht der Amplitude der Schwingung. (Nur bei einer idealisierten ungedämpften Schwingung ohne Reibung ist also die Zeigerlänge konstant.)  
  
−
Mit Hilfe des [[media:Applet_Zeigerdarstellung_animiert.zip|Applets]] läßt sich das gut nachvollziehen. Das folgende Bild ist damit gemacht.
+
===Animation===
 +
Mit Hilfe dieser Animation läßt sich die Zeigerdarstellung nachvollziehen. Wer sich erstmal die Grundlagen von Sinus und Cosinus am Einheitskreis anschauen möchte, kann dies bei der Animation "[[Animation: Sinus und Cosinus im Einheitskreis|Sinus und Cosinus im Einheitskreis]]" tun. Eine Beschreibung des Bogenmaßes gibt die Animation [[Animation: Bogenmaß, Gradmaß und Umdrehungsmaß im Vergleich|Bogenmaß, Gradmaß und Umdrehungsmaß im Vergleich]].
  
−
[[Datei:Zeigerdarstellung.png|framed|none|Die Zeigerdarstellung]]
+
Die Zeit kann man mit dem Schieberegler verändern oder die Animationsgeschwindigkeit größer als Null einstellen.
  
−
==Herleitung der Bewegungsgesetze==
+
An der Spitze des Zeigers kann man seine Länge verändern. Die Drehgeschwindigkeit ω des Zeigers kann man am
−
===Zusammenhang zwischen Winkelgeschwindigkeit, Frequenz und Periodendauer===
+
oberen Schieberegler einstellen.
  
−
Wie bei allen Kreisbewegungen und Schwingungen gilt:
+
{{#widget:Iframe
 +
|url=https://www.geogebra.org/material/iframe/id/shtSrScA/width/957/height/645/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false
 +
|width=957
 +
|height=645
 +
|border=0
 +
}}
  
−
<math>\omega = 2\pi f</math> und <math>T=\frac{1}{f}</math>
+
(Zur [https://www.geogebra.org/material/show/id/shtSrScA Datei] und zum [https://www.geogebra.org/download?lang=de Programm])
  
−
===Das Orts-Gesetz===
+
==Herleitung des Ortsgesetzes==
 +
===Zusammenhang zwischen Winkelgeschwindigkeit (Kreisfrequenz), Frequenz und Periodendauer===
 +
Die Kreisfrequenz oder Winkelgeschwindigkeit entspricht der Geschwindigkeit der Zeigerspitze auf dem Einheitskreis. Sie gibt an, wieviel der Winkel sich im Bogenmaß pro Sekunde ändert.
  
−
Der Ort des Körpers ist gerade die y-Koordinate der Zeigerspitze. Hat sich der Zeiger um den Winkel  <math>\alpha</math> gedreht, so gilt:
+
Die Frequenz gibt die Anzahl der Umdrehungen pro Sekunde, die Periodendauer die Zeit für eine Umdrehung an.
  
−
<math>\sin \alpha = \frac{y}{\hat y} \qquad \Leftrightarrow \qquad y = \hat y \sin \alpha
+
Betrachtet man eine ganze Umdrehung so gilt:
−
</math>
+
:<math>\omega = \frac{\rm Winkel}{\rm Zeit} = \frac{2 \pi}{T}</math>
−
Der Zeiger bewegt sich mit der Winkelgeschwindigkeit  <math>\omega</math>, es gilt also <math>\alpha = \omega t</math>  und damit erhält man:
+
  
−
<math>y = \hat y \sin (\omega t)</math>
+
Was man häufig so umformt:
 +
:{|class="wikitable"
 +
|style="border-style: solid; border-width: 4px "|
 +
<math>\omega = 2\,\pi f</math> und  <math>f=\frac{1}{T}</math>
 +
|}
  
−
===Berechnung des Geschwindigkeitsgesetzes===
+
===Das Orts-Gesetz===
  
−
Die Geschwindigkeit ist die zeitliche Änderungsrate des Ortes, also muss man nach der Zeit ableiten. Dabei muss man die Kettenregel beachten.
+
Der Ort des Körpers ist gerade die y-Koordinate der Zeigerspitze. Hat sich der Zeiger mit der Länge <math>\hat y</math> um den Winkel  <math>\alpha</math> gedreht, so gilt:
  
−
<math>v(t)=\dot s (t) = (\hat y sin(\omega t)\dot) = \hat y cos(\omega t) \omega</math> (Wiederholung: [f(g(t))]'= f'(g(t)) g'(t) )
+
<math>\sin \alpha = \frac{y}{\hat y} \quad \Leftrightarrow \quad y = \hat y \sin \alpha
 +
</math>
  
−
<math> v(t) = \hat y \omega cos(\omega t) = \hat v cos(\omega t)\qquad \qquad \hat v = \hat y \omega </math> ist die maximale Geschwindigkeit.
+
Der Zeiger bewegt sich mit der Winkelgeschwindigkeit <math>\omega</math>, es gilt also <math>\alpha = \omega t</math> und damit erhält man:
−
 
+
−
===Berechnung des Beschleunigungsgesetzes===
+
−
 
+
−
Um die Beschleunigung zu erhalten, muss man die Geschwindigkeit erneut ableiten.
+
−
 
+
−
<math>a=\dot v = \dot{\hat y \omega cos(\omega t)} = \hat y \omega (-sin(\omega t)) \omega</math>
+
−
 
+
−
<math>a(t)=-\hat y \omega^2 sin(\omega t) = \hat a sin(\omega*t)\qquad \qquad \hat a = -\hat y \omega ^2 </math> ist die maximale Beschleunigung.
+
−
 
+
−
==Folgerungen aus den Bewegungsgesetzen==
+
−
===Impuls===
+
−
Der Impuls hängt direkt mit der Geschwindigkeit über <math>p=m \, v</math> zusammen:
+
−
 
+
−
<math>p(t)=m \, \hat y\, \omega \ cos(\omega\, t) \qquad \qquad \hat p = m\, \hat y \,\omega</math> ist der maximale Impuls.
+
−
 
+
−
===Kraft===
+
−
Die Beschleunigung hängt direkt mit der wirkenden Kraft über <math>F=m\ a</math> zusammen, daher folgt:
+
−
 
+
−
<math>F(t)=-m\, \hat y\, \omega^2 \ sin(\omega\, t) = \hat F \sin(\omega\, t)\qquad \qquad \hat F = -m\, \hat y \,\omega ^2</math> ist die maximale Kraft.
+
−
 
+
−
Ausserdem folgt aus der sinusförmigen Bewegung auch der lineare Zusammenhang <math>F=-D\,y</math> von Kraft und Auslenkung, wie bei einer Feder. (Siehe [[Die harmonische Schwingung#Von der Sinusförmigkeit auf den linearen Kraftverlauf|hier]].)
+
−
 
+
−
===Frequenz===
+
−
Die maximal wirkende Rückstellkraft läßt sich auf zwei Arten berechnen. Einmal über die maximale Beschleunigung <math>-\hat y \,\omega^2 </math> und einmal über die maximale Auslenkung <math>\hat y</math>:
+
−
 
+
−
:<math>\hat F = m \,\hat a = -D\,\hat y</math>
+
−
 
+
−
<math>\Rightarrow -m\, \hat y \,\omega^2 = -D \,\hat y </math>.        Teilt man nun noch durch die Amplitude <math>\hat y</math> und die Masse <math>m</math>, so folgt:
+
−
 
+
−
<math>\omega^2= \frac{D}{m}</math>  oder  <math>\omega= \sqrt{\frac{D}{m}}</math>  ;  <math> f = \frac{1}{2\pi}\sqrt{\frac{D}{m}}</math>  ;  <math> T =  2\pi \sqrt{\frac{m}{D}}</math>  Frequenz einer harmonischen Schwingung
+
−
 
+
−
Die Schwingungsdauer, bzw Frequenz folgt aus der Kreisfrequenz mit:
+
−
<math> \omega=2\,\pi\, f </math> und <math> T = \frac{1}{f}</math>
+
−
 
+
−
==Beispiel: Federpendel==
+
−
[[Bild:Federpendel_paint.JPG|thumb|none|Das Federpendel  benöigt für 10 Schwingungen 12s bei einer Amplitude von 9cm.]]
+
−
 
+
−
 
+
−
<math>T=1{,}2</math>
+
−
<math>\omega=\left( \frac {2*\pi}{1{,}2} \right)</math>
+
−
 
+
−
 
+
−
<math>s(t)=9cm*sin(\left( \frac {2*\pi}{1{,}2s} \right)*t</math>
+
−
 
+
−
<math>v(t)=9cm*\left( \frac {2*\pi}{1{,}2s} \right)*cos(\left( \frac {2*\pi}{1{,}2s} \right)*t)</math>
+
−
 
+
−
<math>\hat v = 9cm*\left( \frac {2*\pi}{1{,}2s} \right)= 47\frac{cm}{s}</math>
+
−
 
+
−
==Aufgaben==
+
−
 
+
−
Zu 108.2
+
−
 
+
−
<math>\omega</math>: Winkelgeschwindigkeit <math>f</math>: Umläufe pro Zeit
+
−
 
+
−
z.B.:
+
−
<math>f = 2Hz</math>
+
−
 
+
−
<math>w = 2*\pi*\left( \frac{1}{s} \right)= 4*\pi*\left( \frac{1}{s} \right)</math>
+
−
 
+
−
<math>\Rightarrow \omega=2*\pi*f</math> und weil <math> f=\left( \frac{1}{T} \right)</math>
+
−
 
+
−
 
+
−
<math>    \omega=\left( \frac{2*\pi}{T} \right)</math>
+
  
−
Zu 108.3
+
:{|class="wikitable"
 +
|style="border-style: solid; border-width: 4px "|
 +
<math>y = \hat y \, \sin (\omega t)</math>
 +
|}
  
−
<math>    \phi_0 </math>:  Phasenverschiebung
+
Aus dem Ortsgesetz lassen sich alle [[Die Bewegungsgesetze einer harmonischen Schwingung|Bewegungsgesetze einer harmonischen Schwingung]] ableiten und auch Aussagen zum Energiegehalt und zur Frequenz machen!
  
−
<math>     \phi_0 = 0^\circ </math>:  Schwingung in Phase
+
====Beispiel: Federpendel====
 +
{|
 +
|
 +
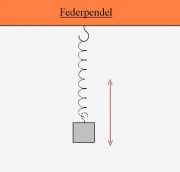
[[Bild:Federpendel_paint.JPG|thumb|none|Das Federpendel  benötigt für 10 Schwingungen 12s bei einer Amplitude von 9cm.]]
 +
|
 +
<math>\hat y = 9\,\rm cm \qquad T=1{,}2\,\rm s \qquad f=\frac{1}{1{,}2\,\rm sec}\approx 0{,}8\,\rm Hz \qquad \omega=\left( \frac {2\pi}{1{,}2 \,\rm s} \right) \approx 5{,}2 \,\rm Hz</math>  
  
−
<math>     \phi_0 = \pi \, (180^\circ\!) </math>: gegenphasig
+
<math>y(t)=9\,\rm cm \cdot sin( 5{,}2 \,\rm Hz \cdot t)</math>
 +
|}
  
 
==Links==
 
==Links==
−
*[[media:Applet_Zeigerdarstellung.zip|Applet zur Zeigerdarstellung]]
 
 
*[http://www.walter-fendt.de/ph14d/fadenpendel.htm Applet zur Sinuskurve des Ortsdiagramms eines Pendels (W.Fendt)]
 
*[http://www.walter-fendt.de/ph14d/fadenpendel.htm Applet zur Sinuskurve des Ortsdiagramms eines Pendels (W.Fendt)]
 
*[http://www.walter-fendt.de/ph14d/federpendel.htm Applet zum Federpendel (W.Fendt)]
 
*[http://www.walter-fendt.de/ph14d/federpendel.htm Applet zum Federpendel (W.Fendt)]
 
*[http://de.wikipedia.org/wiki/Zeigerdiagramm Wikipedia: Zeigerdiagramm]
 
*[http://de.wikipedia.org/wiki/Zeigerdiagramm Wikipedia: Zeigerdiagramm]

Aktuelle Version vom 13. Juni 2023, 16:40 Uhr

(Kursstufe > Mechanische Schwingungen)


Ausgehend von experimentellen Beobachtungen stellt man ein mathematisches Modell auf, mit dem man die Bewegung einer Schwingung beschreiben kann. Ob dieses sogenannte Zeigermodell für eine Schwingung zutrifft, kann man wiederum nur experimentell untersuchen.

Das Vorgehen ist also deduktiv, ein Modell wird im Experiment überprüft.

Alle Schwingungen, die sich mit dem Zeigermodell beschreiben lassen, heißen harmonische Schwingungen.


Versuch: Ein Sandpendel

Aufbau
Versuchsaufbau des Sandpendels (1)

Ein Trichter wird mit Sand gefüllt und in Schwingungen versetzt. Unter dem Trichter befindet sich eine Tapete, die dann quer zur Schwingungsrichtung unter dem Pendel weggezogen wird.

Beobachtung
Versuchsergebnis des Sandpendels(2)

Es entsteht eine Wellenlinie. (Siehe Bild 2)

Erklärung

Diese Wellenlinie ist gerade das Zeit-Ort Diagramm einer Schwingung, denn sie gibt an wann der Körper wo ist. Die Ortsfunktion scheint eine Sinusfunktion zu sein, an der man die Amplitude und die Periode ablesen kann.

Versuch: Projektion der Kreisbewegung

Aufbau

  • Versuchsaufbau mit einem Zeunerwagen und einer Glühlampe

  • oder so...

  • Das vertikale Federpendel

  • und das horizontale Federpendel.

Direkt neben den schwingenden Wagen oder das schwingende Männchen wird ein Motor mit einem exzentrischen Stift befestigt.

Eine Lampe oder ein Diaprojektor wirft von beiden einen Schatten an die Wand.

Man versucht nun zu erreichen, dass der Schatten des Wagens (oder des Männchens) sich genauso wie der Schatten des sich drehenden Stiftes bewegt. Zunächst stellt man dazu die Drehgeschwindigkeit des Motors in etwa ein. Die Frequenz des Federpendels ist aber exakter regulierbar, indem man z.B. mit Knete die Masse vergrößert.

Beobachtung

Wenn die Umlaufzeit genau mit der Periodendauer der Schwingung übereinstimmt und die Amplitude der Schwingung genausogroß ist wie der Stift von der Mitte entfernt ist und man im richtigen Moment losläßt, dann bewegen sich die Schatten ganz gleich auf der Wand hin und her.

Video von der Seite. Video der Schattenprojektion.

Folgerung

Man kann den Ort eines harmonischen Schwingers durch die Projektion einer Kreisbewegung beschreiben!

Die Zeigerdarstellung

Ausgehend von dem Ergebnis des Projektionsversuchs, beschreibt man eine harmonische Schwingung durch einen drehenden Zeiger.

  • Die Projektion des Zeigers auf die y-Achse ist die Elongation des schwingenden Körpers.
  • Der Zeiger dreht sich mit konstanter Winkelgeschwindigkeit gegen den Uhrzeigersinn.
  • Die Länge des Zeigers entspricht der Amplitude der Schwingung. (Nur bei einer idealisierten ungedämpften Schwingung ohne Reibung ist also die Zeigerlänge konstant.)

Animation

Mit Hilfe dieser Animation läßt sich die Zeigerdarstellung nachvollziehen. Wer sich erstmal die Grundlagen von Sinus und Cosinus am Einheitskreis anschauen möchte, kann dies bei der Animation "Sinus und Cosinus im Einheitskreis" tun. Eine Beschreibung des Bogenmaßes gibt die Animation Bogenmaß, Gradmaß und Umdrehungsmaß im Vergleich.

Die Zeit kann man mit dem Schieberegler verändern oder die Animationsgeschwindigkeit größer als Null einstellen.

An der Spitze des Zeigers kann man seine Länge verändern. Die Drehgeschwindigkeit ω des Zeigers kann man am oberen Schieberegler einstellen.

(Zur Datei und zum Programm)

Herleitung des Ortsgesetzes

Zusammenhang zwischen Winkelgeschwindigkeit (Kreisfrequenz), Frequenz und Periodendauer

Die Kreisfrequenz oder Winkelgeschwindigkeit entspricht der Geschwindigkeit der Zeigerspitze auf dem Einheitskreis. Sie gibt an, wieviel der Winkel sich im Bogenmaß pro Sekunde ändert.

Die Frequenz gibt die Anzahl der Umdrehungen pro Sekunde, die Periodendauer die Zeit für eine Umdrehung an.

Betrachtet man eine ganze Umdrehung so gilt:

[math]\omega = \frac{\rm Winkel}{\rm Zeit} = \frac{2 \pi}{T}[/math]

Was man häufig so umformt:

[math]\omega = 2\,\pi f[/math] und [math]f=\frac{1}{T}[/math]

Das Orts-Gesetz

Der Ort des Körpers ist gerade die y-Koordinate der Zeigerspitze. Hat sich der Zeiger mit der Länge [math]\hat y[/math] um den Winkel [math]\alpha[/math] gedreht, so gilt:

[math]\sin \alpha = \frac{y}{\hat y} \quad \Leftrightarrow \quad y = \hat y \sin \alpha [/math]

Der Zeiger bewegt sich mit der Winkelgeschwindigkeit [math]\omega[/math], es gilt also [math]\alpha = \omega t[/math] und damit erhält man:

[math]y = \hat y \, \sin (\omega t)[/math]

Aus dem Ortsgesetz lassen sich alle Bewegungsgesetze einer harmonischen Schwingung ableiten und auch Aussagen zum Energiegehalt und zur Frequenz machen!

Beispiel: Federpendel

Das Federpendel benötigt für 10 Schwingungen 12s bei einer Amplitude von 9cm.

[math]\hat y = 9\,\rm cm \qquad T=1{,}2\,\rm s \qquad f=\frac{1}{1{,}2\,\rm sec}\approx 0{,}8\,\rm Hz \qquad \omega=\left( \frac {2\pi}{1{,}2 \,\rm s} \right) \approx 5{,}2 \,\rm Hz[/math]

[math]y(t)=9\,\rm cm \cdot sin( 5{,}2 \,\rm Hz \cdot t)[/math]

Links

Von „http://www.schulphysikwiki.de/index.php?title=Beschreibung_einer_harmonischen_Schwingung_mit_der_Zeigerdarstellung&oldid=17172“