Beschreibung einer harmonischen Schwingung mit der Zeigerdarstellung
Ausgehend von experimentellen Beobachtungen stellt man ein mathematisches Modell auf, mit dem man die Bewegung einer Schwingung beschreiben kann. Ob dieses sogenannte Zeigermodell für eine Schwingung zutrifft, kann man wiederum nur experimentell untersuchen.
Das Vorgehen ist also deduktiv, ein Modell wird im Experiment überprüft.
Alle Schwingungen, die sich mit dem Zeigermodell beschreiben lassen, heißen harmonische Schwingungen.
Inhaltsverzeichnis
Versuch: Ein Sandpendel
Aufbau:
Siehe Bild 1
Beobachtung:
Es entsteht eine Wellenlinie. (Siehe Bild 2)
Erklärung
Diese Wellenlinie ist gerade das Zeit-Ort Diagramm einer Schwingung, denn sie gibt an wann der Körper wo ist. Die Ortsfunktion scheint eine Sinusfunktion zu sein, an der man die Amplitude und die Periode ablesen kann.
Versuch: Projektion der Kreisbewegung
Aufbau:
Variation der Drehgeschwindigkeit oder Variation der Schwingung durch Veränderung der Masse und Feder. Die Veränderung der Schwingung ist exakter durchführbar!
Beobachtung:
Text Text Text Text Text Text TextText Text Text Text Text Text Text Text Text Text Text
Erklärung
Text Text Text Text Text Text TextText Text Text Text Text Text Text Text Text Text Text
Die Zeigerdarstellung
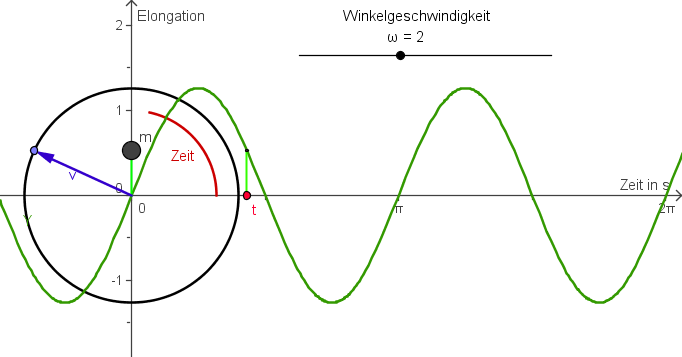
Ausgehend von dem Ergebnis des Projektionsversuchs, beschreibt man eine harmonische Schwingung durch einen drehenden Zeiger.
- Die Projektion des Zeigers auf die y-Achse ist die Elongation des schwingenden Körpers.
- Der Zeiger dreht sich mit konstanter Winkelgeschwindigkeit gegen den Uhrzeigersinn.
- Die Länge des Zeigers entspricht der Amplitude der Schwingung. (Nur bei einer idealisierten ungedämpften Schwingung ohne Reibung ist also die Zeigerlänge konstant.)
Mit Hilfe des Applets läßt sich das gut nachvollziehen. Das folgende Bild ist damit gemacht.
Herleitung der Bewegungsgesetze
Zusammenhang zwischen Winkelgeschwindigkeit, Frequenz und Periodendauer
Wie bei allen Kreisbewegungen und Schwingungen gilt:
[math]\omega = 2\pi f[/math] und [math]T=\frac{1}{f}[/math]
Das Orts-Gesetz
Der Ort des Körpers ist gerade die y-Koordinate der Zeigerspitze. Hat sich der Zeiger um den Winkel [math]\alpha[/math] gedreht, so gilt:
[math]\sin \alpha = \frac{y}{\hat y} \qquad \Leftrightarrow \qquad y = \hat y \sin \alpha [/math] Der Zeiger bewegt sich mit der Winkelgeschwindigkeit [math]\omega[/math], es gilt also [math]\alpha = \omega t[/math] und damit erhält man:
[math]y = \hat y \sin (\omega t)[/math]
Berechnung des Geschwindigkeitsgesetzes
Die Geschwindigkeit ist die zeitliche Änderungsrate des Ortes, also muss man nach der Zeit ableiten. Dabei muss man die Kettenregel beachten.
[math]v(t)=\dot s (t) = (\hat y sin(\omega t)\dot) = \hat y cos(\omega t) \omega[/math] (Wiederholung: [f(g(t))]'= f'(g(t)) g'(t) )
[math] v(t) = \hat y \omega cos(\omega t) = \hat v cos(\omega t)\qquad \qquad \hat v = \hat y \omega [/math] ist die maximale Geschwindigkeit.
Für den Impuls folgt direkt:
Berechnung des Beschleunigungsgesetzes
Um die Beschleunigung zu erhalten, muss man die Geschwindigkeit erneut ableiten.
[math]a=\dot v = \dot{\hat y \omega cos(\omega t)} = \hat y \omega (-sin(\omega t)) \omega[/math]
[math]a(t)=-\hat y \omega^2 sin(\omega t) = \hat a sin(\omega*t)\qquad \qquad \hat a = -\hat y \omega ^2 [/math] ist die maximale Beschleunigung.
Folgerungen aus den Bewegungsgesetzen
Impuls
Der Impuls hängt direkt mit der Geschwindigkeit über [math]p=m v[/math] zusammen:
[math]p(t)=m \hat y \omega cos(\omega t) \qquad \qquad \hat p = m\hat y \omega[/math] ist der maximale Impuls.
Kraft
Die Beschleunigung hängt direkt mit der wirkenden Kraft zusammen, daher folgt:
[math]F(t)=-m \hat y \omega^2 sin(\omega t) = \hat F sin(\omega t)\qquad \qquad \hat F = -m \hat y \omega ^2[/math] ist die maximale Kraft.
Schreibt man die Gleichung etwas um, so erkennt man den Zusammenhang zwischen Kraft F und Auslenkung y:
[math]F=-m \hat y \omega^2 sin(\omega t) = -m \omega^2 y[/math]
Die Kraft ist also proportional zur Auslenkung mit der Federkonstanten [math]D=m \omega^2[/math]!
Beispiel: Federpendel
[math]T=1{,}2[/math]
[math]\omega=\left( \frac {2*\pi}{1{,}2} \right)[/math]
[math]s(t)=9cm*sin(\left( \frac {2*\pi}{1{,}2s} \right)*t[/math]
[math]v(t)=9cm*\left( \frac {2*\pi}{1{,}2s} \right)*cos(\left( \frac {2*\pi}{1{,}2s} \right)*t)[/math]
[math]\hat v = 9cm*\left( \frac {2*\pi}{1{,}2s} \right)= 47\frac{cm}{s}[/math]
Aufgaben
Zu 108.2
[math]\omega[/math]: Winkelgeschwindigkeit [math]f[/math]: Umläufe pro Zeit
z.B.: [math]f = 2Hz[/math]
[math]w = 2*\pi*\left( \frac{1}{s} \right)= 4*\pi*\left( \frac{1}{s} \right)[/math]
[math]\Rightarrow \omega=2*\pi*f[/math] und weil [math] f=\left( \frac{1}{T} \right)[/math]
[math] \omega=\left( \frac{2*\pi}{T} \right)[/math]
Zu 108.3
[math] \phi_0 = Phasenverschiebung[/math] [math] \phi_0 = 0° = Schwingung in Phase[/math] [math] \phi_0 =LaTex: \pi*(180°) = gegenphasig[/math]