Die Maxwellschen Gleichungen: Unterschied zwischen den Versionen

Version vom 22. Juni 2017, 18:05 Uhr

(Kursstufe > Elektro-Magnetismus)

Michael Faraday (1791 bis 1867)

James Maxwell (1831 bis 1879)

Mit Hilfe von nur 4 Gleichungen werden alle elektrischen, magnetischen und optischen Phänomene beschrieben.

Zwei Gleichungen beschreiben die Zusammenhänge der Elektrizität und des Magnetismus bei zeitlich unveränderlichen Situationen.

• In der Elektrostatik beschreibt das "Gaußsche Gesetz" den Zusammenhang von Ladung und Polarisation der Gegenstände mit dem elektrischen Feld.
• Das "Gaußsche Gesetz der Magnetostatik" beschreibt den Zusammenhang zwischen der Magnetisierung von Gegenständen und dem magnetischen Feld.

Eine typische Frage wäre zum Beispiel die nach der elektrischen Feldstärke eines geladenen Luftballons in einem bestimmten Abstand oder nach der magnetischen Feldstärke eines Stabmagneten mit einer bestimmten Magnetisierung.

Die zwei anderen Gleichungen beschreiben die Elektrodynamik, in denen sich die physikalischen Größen der Elektro- und Magnetostatik zeitlich ändern.

• Das "Induktionsgesetz" formuliert wie elektrische Felder um sich verändernde magnetische Felder oder die Magnetisierung verändernde Gegenstände entstehen;
• das "erweiterte Ampèresche Gesetz" wie sich magnetische Felder um bewegte Ladungsträger (Strom), um sich verändernde elektrische Felder und um die Polarisierung verändernde Gegenstände entstehen.

Die Gleichungen der Elektrodynamik beschreiben zusammen das wechselseitige Erzeugen von elektrischem und magnetischem Feld einer elektro-magnetischen Welle und damit auch die Phänomene der Optik.

Michael Faraday und James Clerk Maxwell

Der 1831 in Edinburgh geborene James Maxwell war, bis zu seinem Tod 1879, einer der bedeutensten Physiker des zwanzigsten Jahrhunderts. Zu seinen wichtigsten Entdeckungen zählen die Geschwindigkeitsverteilung von Gasmolekülen (Maxwellverteilung), die Vereinigung elektrischer und magnetischer Phänomene zum Elektromagnetismus (Maxwellsche Gleichungen), sowie Theorien über die (elektromagnetische)-Wellenartigkeit des Lichts.

"Ich [bemerkte] bald, daß Faradays Methode, die Vorgänge zu betrachten, ihrem Wesen nach ebenfalls eine mathematische ist, obzwar er sich nicht der üblichen mathematischen Symbole bedient. Ich sah auch, daß seine Methode die Möglichkeit bietet, sie in die Sprache der der gewöhnlichen Mathematik zu übersetzen [...]."[3] "Ich fand auch, dass einige der fruchtbarsten von Mathematikern entdeckten Untersuchungsmethoden mit Faradays Herangehensweise wesentlich besser auszudrücken waren. [...] Somit finden viele mathematischen Entdeckungen von Laplace, Poisson, Green und Gauß den richtigen Platz in dieser Abhandlung und ihren angemessenen Ausdruck im Sinne der hauptsächlich von Faraday entwickelten Konzeptionen. "[4]

James Maxwell

Felder und Materie

Um Felder und Materie physikalisch zu beschreiben, benötigt man messbare Größen.

Die charakterisierenden Größen der Felder sind in den Maxwell-Gleichungen die elektrische Feldstärke [math]\vec E [/math] und die magnetische Feldstärke [math]\vec H [/math].

Die elektrischen Eigenschaften von Materie werden durch die Menge der elektrischen Ladung [math]Q[/math] und die Polarisation [math]\vec P[/math], die magnetischen Eigenschaften durch die magnetische Polarisation [math]\vec J[/math] bestimmt.

Wie man sieht, tauchen in den "Hieroglyphen" der Gleichungen sowohl die elektrische Ladung als auch die magnetische und elektrische Feldstärke auf, aber die Polarisation und die Magnetisierung sucht man vergebens. Sie sind in den noch zu klärenden Größen [math]\vec D[/math] und [math]\vec B[/math] "versteckt".

Elektro- und Magnetostatik

Quellen und Senken des elektrischen Feldes

Qualitativ: Feldlinien, Ladungen und Polarisierungslinien

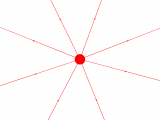
Stellt man die Feldstärke mit Hilfe von Feldlinien dar, so kann man eine anschauliche Form der Maxwellschen Gleichung für die Elektrostatik gewinnen:

• 

  Ein positiv geladener Ball hat ein Zentralfeld um sich.

• 

  Mit einer negativen Ladung kehrt sich die Richtung der Feldstärke um.

• 

  Ein Plattenkondensator mit sehr großem Plattenabstand erzeugt ein Dipolfeld.

• Feldlinien beginnen bei positiven Ladungen und enden bei negativen Ladungen.
• Positive Ladungen sind die Quellen und negative Ladungen die Senken der Feldstärke
• Je "dichter" die Feldlinien, desto größer ist die Feldstärke.

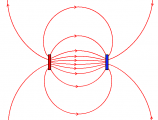
Dabei sind mit "Ladungen" sowohl geladene Gegenstände als auch Polarisierungsladungen gemeint. Polarisierte Gegenstände erzeugen ebenso ein elektrisches Feld. Bei einem dauerhaft polarisierten Elektret sind sogar ausschließlich Polarisierungsladungen vorhanden. Dabei erkennt man den Zusammenhang zwischen Feldstärke, Polarisierungsladungen und Polarisierung:

• 

  Die Dipole des Elektrets sind ausgerichtet.

• 

  An den Rändern bildet sich genausoviel positive wie negative Polarisierungsladung. Die Polarisierung verläuft von negativer zu positiver Polarisierungsladung.

• 

  Die Polarisierungsladungen erzeugen ein elektrisches Dipolfeld.

• 
• 

  Man könnte den Elektret auch außen herum biegen...

• 

  und erhält die gleichen Polarisierungsladungen und das gleiche Feld.

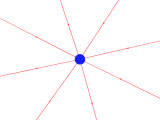
• Polarisierungslinien beginnen bei negativen Polarisierungsladungen und enden bei positiven Polarisierungsladungen.
• Negative Polarisierungsladungen sind die Quellen und positive Polarisierungsladungen die Senken der Polarisierung.

Quantitativ: Feld-Fluß durch geschlossene Flächen

Indem man geschlossene Flächen, wie Kugeloberflächen oder Quaderoberflächen, betrachtet, kann man das anschauliche Bild der Feldlinien und Polarisierungslinien in eine mathematische Form bringen. Genau diese Verbindung der anschaulichen Vorstellung von Faraday mit der Mathematik von Vektorfeldern hat Maxwell zum ersten Mal hergestellt.

• 

  Die Ladung ist positiv, die Feldlinien gehen aus den Kugelflächen heraus. Die äußere Oberfläche ist größer, aber dort ist die Feldstärke geringer als Innen. Durch beide Flächen gehen die gleiche Anzahl an Feldlinien.

• 

  Bei einer negativen Ladung gehen die Feldlinien in die geschlossene Fläche hinein.

• 

  Aus der Fläche A1 gehen genauso viele Feldlinien heraus wie in A2 hinein. In die Fläche A3 gehen genauso viele Feldlinien rein wie raus.

Die Feldstärke entspricht der Feldliniendichte. Das Produkt aus Feldstärke und Fläche ist also ein Maß für die Anzahl der Feldlinien durch die Fläche. Man nennt es auch den Fluß der Feldstärke durch eine Fläche.

Der Feldstärkefluß geht aus der Fläche heraus, wenn sie eine positive Ladung enthält und hinein, wenn sie eine negative Ladung enthält. Enthält eine geschlossene Fläche keine Ladung, so ist der mittlere Feldstärkefluß Null.

Die sogenannte "elektrische Feldkonstante" [math]\epsilon_0[/math] beschreibt, wie die Einheiten der drei Größen zusammenhängen: Bei einer mittleren Feldstärke von 1 N/C auf einer Oberfläche von 1m² Größe beträgt die von der Fläche umschloßene Ladung [math]8{,}85 \cdot 10^{-12} \mathrm C[/math]:

Häufig zerlegt man die geschlossene Fläche in Teilflächen auf denen die Feldstärke konstant ist. (Beispiele für Anwendungen.)

Siehe: Felderzeugende Ladung und Feldstärke Weitere Abstraktion:

[math]{Q \over A}=\epsilon_0 E[/math]

[math]Q = \epsilon_0 E \, A = \epsilon_0 \int E \cdot dA[/math] (bei genauerer Betrachtung)

[math]Q = \epsilon_0 \int E \cdot dA[/math]

Die Summe der elektrischen Feldstärke von allen Punkten einer geschlossenen 
Fläche entspricht der elektrischen Ladung innerhalb dieser Fläche.

Material im elektrischen Feld:

Auch die Enden der Polarisierung sind Quellen und Senken der elektrischen Feldstärke. "Es gehen genausoviele Polarisierungslinien hinein wie elektrische Feldstärkelinien heraus."

[math]\epsilon_0 \int E \cdot dA = -\int P \cdot dA[/math]

An den Enden des polarisierten Gegenstandes befinden sich Polarisierungsladungen, welche die Quellenstärke angeben:

[math]Q_{pol} = -\int P \cdot dA[/math]

Zusammen mit den elektrischen Ladungen gibt es also zwei Möglichkeiten Quellen und Senken der elektrischen Feldstärke zu erzeugen:

[math]\epsilon_0 \int E \cdot dA = Q + Q_{pol} \qquad \text{mit} \qquad Q_{pol} = -\int P \cdot dA[/math]

Es ist üblich die Polarisierung und die elektrische Feldstärke zu einer Größe, der "elektrischen Flusdichte D" zusammenzufassen. Die elektrische Flussdichte entspricht in einfachen Fällen, wie einem Kondensator, der Flächenladungsdichte.

[math] \int (\epsilon_0 E + P )\cdot dA = Q [/math]

[math]\vec{D} = \varepsilon_0 \vec{E} + \vec{P}[/math]

[math] \int D \cdot dA = Q [/math]

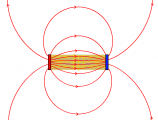
Die 4. Maxwellsche Gleichung (Erzeugung von magnetischen Feldern durch Magnetisierung)

vergrößern

Die Enden der Magnetisierung sind Quellen und Senken der magnetischen Feldstärke. "Es gehen genausoviele Magnetisierungslinien hinein wie magnetische Feldstärkelinien heraus."

[math]\mu_0 \int E \cdot dA = -\mu_0\, \int M \cdot dA[/math]

Die Quellenstärke wird also durch die Stärke der Pole gegeben. Diese Polstärke kann man auch als "magnetische Ladung" bezeichnen:

[math]Q_{mag}= -\mu_0 \, \int M \cdot dA[/math]

Im Gegensatz zum elektrischen Feld gibt es keine magnetischen Monopole, deswegen kann man magnetische Felder nur durch Magnetisierung erzeugen:

[math]\mu_0 \int E \cdot dA = Q_{mag} \qquad \textrm{mit} \qquad Q_{mag} = -\mu_0\, \int M \cdot dA[/math]

Es ist üblich die Magnetisierung und die magnetische Feldstärke zu einer Größe, der "magnetischen Flussdichte B" zusammenzufassen. Die magnetische Flussdichte ist die entscheidende Größe für die Lorentzkraft und die Induktion.

[math] \int \mu_0 (H+M) \cdot dA = 0[/math]

[math]\vec{B} = \mu_0 (\vec H + \vec M)[/math]

[math] \int B \cdot dA = 0 [/math]

Die Linien der magnetischen Flußdichte bilden daher stets geschlossene Kreise.

Elektromagnetismus

Die 1. Maxwellsche Gleichung / Durchflutungsgesetz (Erzeugung von magnetischen Wirbelfeldern)

Etwas analoges zu einem elektrischen Wirbelfeld findet man im magnetischen Feld bei den magnetischen Wirbelfeldern. Wie bereits bekannt entstehen diese um elektrische Ströme. (siehe Die magnetische Feldstärke.)

Allgemeiner gefasst:

[math]Hl = I[/math] entspricht [math]\int H \cdot ds = I[/math]

Der Verschiebungsstrom

Gedankenversuch: Laden eines Kondensators

Aufbau

Ein Kondensator wird mit einer Batterie geladen.

Ablauf

Nach dem Ampereschen Gesetz müsste sich überall entlang des Kabels ein magnetisches Wirbelfeld bilden, solange der Kondensator aufgeladen wird und dazu ein Strom fließt. Die Vorstellung, das dieses magnetische Wirbelfeld allerdings genau beim Kondensator aufhört und direkt danach wieder beginnt, wirkt allerdings befremdlich.

Aus diesem Grund erweiterte Maxwell das Amperesche Gesetz um den so genannten Verschiebungsstrom: Wir betrachten zunächst die Ladung des Kondensators, indem wir uns eine Fläche um eine der Platten vorstellen: Nach 1. Maxwellschen Gleichung erhalten wir:

[math]Q = \epsilon_0 \int E \cdot dA[/math]

Die leiten wir nach der Zeit ab:

[math]{dQ \over dt} = \epsilon_0 {d \over dt}\int E \cdot dA[/math]

Da die zeitliche Ableitung der Ladung auch als Strom gesehen werden kann:

[math]I_v = \epsilon_0 {d \over dt}\int E \cdot dA[/math]

Diesen Verschiebungsstrom setzen wir nun wieder in das Amperesche Gesetz ein:

[math]\int H \cdot ds = I + \epsilon_0 {d \over dt}\int E \cdot dA[/math]

Um ein elektrischen Strom oder um ein sich änderndes elektrisches Feld
entsteht also auch ein magnetisches Wirbelfeld.

Die 2. Maxwellsche Gleichung / Induktionsgesetz (Erzeugung von elektrischen Wirbelfeldern)

Versuch: Elektrisches Wirbelfeld (Elektrodenlose Ringentladung)

Aufbau

Eine mit Neon gefüllte Glaskugel ist von einer Ringspule umgeben. Man legt eine hochfrequente (ca.10000Hz) Welchselspannung mit etwa 400 V an die Spule und erzeugt so ein sich schnell änderndes torusförmiges magnetisches Wechselfeld.

• 

  Bild 1

• 

  Rückseite der Geräte

• 

  Der alternative Aufbau mit einer Funkenstrecke

• 

  Hier wird die Eingangsspannung mit einem [math]320\,\rm \Omega[/math] Widerstand geregelt.

Beobachtung

• 

  Bild 1

• 
• 
• 
• 

  Mit der Funkenstrecke leuchtet das Gas so intensiv, dass man es schlecht beobachten kann.

• 

  Mit der regelbaren Eingangsspannung kann man die Intensität des Leuchtens herunterregeln.

Video des Versuchs.

Überlegung für Potentialfelder

Ein geschlossener rosa Kreis entsteht innerhalb der Glaskugel. Dies lässt auf ein elektrisches Feld schließen. Da dies jedoch rund ist, kann es sich nicht um ein Potenzialfeld handeln, sonder nur um ein elektrisches Wirbelfeld.

[math]U_{1,2} = \phi_1 - \phi_2 = \int_{P_1}^{P_2} E \cdot ds[/math]

Bei gleichem Anfangs- und Endpunkt:

[math]\int_{P_1}^{P_1} E \cdot ds = 0\quad \text{also}\quad \oint_{} E \cdot ds = 0[/math]

Im Wirbelfeld

Für ein Wirbelfeld wird dieses geschlossene Integral also nicht null ergeben, sondern eine andere induzierte Spannung: [math]\oint_{} E_{ind} \cdot ds = U_{ind}[/math]

Mit [math]U_{ind} = -{d \Phi \over dt}[/math]:

[math]\oint_{} E_{ind} \cdot ds = -{d \Phi \over dt}[/math]

Da [math]\Phi = A \cdot B \quad \text{genauer}\quad \Phi = \int B \cdot dA[/math]:

[math]\oint_{} E_{ind} \cdot ds = -{d \over dt}\int B \cdot dA[/math]

Um ein sich änderndes Magnetfeld entsteht also ein elektrisches Wirbelfeld.

Links

• Video und Versuchsaufbau elektrodenlose Ringentladung (Landesbildungsserver BaWü)
• Elektrodenlose Ringentladung Vorlesungssammlung Physik der Universität Ulm
• youtube: Tesla Trafo(Leybold)

Fußnoten

1. ↑ Ein abgewandeltes Faust-Zitat von Ludwig Boltzmann über die Maxwellschen Gleichungen, aus: Vorlesungen, II Teil, Vorwort, zitiert nach [Sim] , S.347
2. ↑ Aus einem Brief von Michael Faraday an Maxwell. 1857. , zitiert nach [Sim] , S.346
3. ↑ Aus dem Vorwort von [Max] S. ix/x. (Direkter Link). 1857. , Übersetzung aus [Sim] , S.342
4. ↑ "I also found that several of the most fertile methods of research discovered by the mathematicians could be expressed much better in terms of ideas derived from Faraday than in their original form. [...] Hence many of the mathematical discoveries of Laplace, Poisson, Green and Gauss find their proper place in this treatise, and their appropriate expression in terms of conceptions mainly derived from Faraday." Aus dem Vorwort von [Max] S. xi. (Direkter Link). 1857.