Ladung als Quellenstärke und der Fluss eines Feldes: Unterschied zwischen den Versionen
K (hat „Ladung als Quellstärke und der Fluß eines Feldes“ nach „Ladung als Quellenstärke und der Fluß eines Feldes“ verschoben: Schreibfehler) |
K (→Feldfluß, Quellenstärke und Feldkonstanten) |
||
| Zeile 76: | Zeile 76: | ||
Bei einer Feldstärke von 1 N/C und einer Oberfläche von 1m^2 beträgt die von der Fläche umschloßene Ladung <math>8{,}85 \cdot 10^{-12} \textstyle C</math>. | Bei einer Feldstärke von 1 N/C und einer Oberfläche von 1m^2 beträgt die von der Fläche umschloßene Ladung <math>8{,}85 \cdot 10^{-12} \textstyle C</math>. | ||
| − | Dies ist nun die Präzisierung, die wir gesucht haben! Anstatt zu sagen, dass die | + | Dies ist nun die Präzisierung, die wir gesucht haben! Anstatt zu sagen, dass die ''Feldlinien dicht liegen'' beschreiben wir das mit einem ''großen Feldfluß durch die Fläche''. Den Fluß des elektrischen Feldes legen wir als <math>\epsilon_0 \, E \, A</math> fest. |
| − | + | ||
| − | + | ||
Für schwere und magnetische Felder läßt sich das Ergebnis ebenso zusammenfassen: | Für schwere und magnetische Felder läßt sich das Ergebnis ebenso zusammenfassen: | ||
| Zeile 84: | Zeile 82: | ||
Der Fluß<ref name="Fluß"/>eines Feldes durch eine Feldfläche entspricht | Der Fluß<ref name="Fluß"/>eines Feldes durch eine Feldfläche entspricht | ||
der von der Fläche umschlossenen Ladung: | der von der Fläche umschlossenen Ladung: | ||
| − | <math> \frac{1}{4\pi \,G} \ g \, A = m \qquad \epsilon_0 \, E \, A = Q \qquad \mu_0 \, H \, A = Q_m</math> | + | <math> \frac{1}{4\pi \,G} \ g \, A = m \qquad \epsilon_0 \, E \, A = Q \qquad \mu_0 \, H \, A = Q_m</math> |
==Quellenstärke und Feldfluß für beliebige Felder== | ==Quellenstärke und Feldfluß für beliebige Felder== | ||
Version vom 5. April 2012, 12:01 Uhr
Inhaltsverzeichnis
Fragestellung: Feldstärke und "Feldliniendichte"
Die Fragestellung lautet:
- Wie kann man bei gegebener Verteilung der Ladung (magnetische, elektrische oder schwere) die Feldstärke an einer Stelle berechnen?
Aus unseren bisherigen Erfahrungen können wir zwei qualitative Aussagen machen:
- Je kleiner der Abstand von der Ladung, desto größer die Feldstärke.
- Je größer die felderzeugende Ladung, desto größer die Feldstärke.
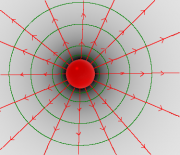
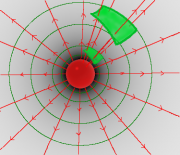
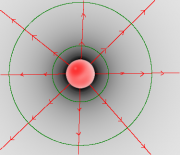
Um zu einer vorläufigen Antwort zu kommen, schaut man sich die graphische Darstellung eines Zentralfeldes nochmal genau an. Vom geladenen Gegenstand gehen die Feldlinien aus und durchstoßen orthogonal die Feldflächen.
An den Orten mit großer Feldstärke liegen die gezeichneten Linien dichter beisammen. Wie kann man das präzisieren?
Die Feldflächen haben mit zunehmendem Abstand von der Ladung eine immer größeren Flächeninhalt. Die Anzahl der sie durchdringenden Linien bleibt aber immer gleich. Als "Dichte" der Feldlinien könnte man also die "Anzahl der Linien" pro Fläche verstehen.
Stellt man sich eine Bewegung entlang der Linien vor, so fließt sie parallel zu den Linien aus der Ladung heraus durch die Flächen. Dieser "Feldfluß" ist überall gleichgroß. Mit größerem Abstand zur Ladung werden die Flächen größer und somit wird der Fluß pro Fläche, die "Flußdichte", kleiner.
Feldstärke eines Zentralfeldes
Das Zentralfeld ist besonders übersichtlich und auch leicht in einem Experiment zu realisieren. Deswegen betrachten wir erst diesen Spezialfall.
Feldstärke und Fluß
Wenn die Flußdichte oder "Feldliniendichte" ein Maß für die Feldstärke sein soll, dann muß in dem Maße wie der Inhalt der Feldfläche zunimmt, die Feldstärke abnehmen. Das soll durch eine Messung an einem Zentralfeld überprüft werden.
Wie könnte die Feldstärke abnehmen?
- Antiproportional zum Radius: Doppelter Abstand --> halbe Feldstärke
- Antiproportional zum Inhalt der Feldfläche: Doppelter Abstand (Vierfacher Flächeninhalt [math]A=4 \pi r^2[/math]) --> viertel Feldstärke
Zur Überprüfung messen wir die Kraftwirkung auf einen Probenordpol im Feld des Nordpols eines langen Stabmagneten. Wir stellen fest: Verdoppelt man den Abstand der Pole und vervierfacht damit den Inhalt der Feldfläche, so verringert sich die Feldstärke auf ein Viertel!
Das Produkt aus Feldstärke und Flächeninhalt ist also für alle Feldflächen gleichgroß. Es gibt anschaulich an, "wieviele" Feldlinien durch die Fläche verlaufen und ist ein Maß für den Fluß des Feldes.
Auch für das elektrische Feld kann man diesen Zusammenhang messen und findet das gleiche Ergebnis! Für das Schwerefeld gilt dies ebenso. Schon Newton kannte diesen Zusammenhang für das Gravitationsfeld. Er ergibt sich aus der Beobachtung der Planeten.
Die Feldstärke um eine Ladung nimmt in dem Maße ab, wie der Inhalt der Feldlfläche zunimmt. Der Feldfluß[1] ist überall gleich: [math]g \sim \frac{1}{A} [/math] oder [math]g \, A[/math] ist konstant "Doppelte Fläche --> Halbe Feldstärke" [math]E \sim \frac{1}{A}[/math] oder [math]E \, A[/math] ist konstant [math]H \sim \frac{1}{A}[/math] oder [math]H \, A[/math] ist konstant
Feldstärke und felderzeugende Ladung
Wieder kann man im Falle der magnetischen Ladungen relativ einfach messen. Dazu verdoppeln wir die felderzeugende Ladung des Stabmagneten, indem wir einen zweiten parallel dazu befestigen. Jetzt messen wir wieder die Kraftwirkung auf den Probenordpol.
Wir stellen fest: Bei der doppelten felderzeugenden Ladung ist die Kraftwirkung und somit auch die Feldstärke doppelt so groß!
Die Ladung beschreibt die Quellenstärke des Feldflußes, also "wieviele" Feldlinien aus der Ladung herauskommen.
Dieser Zusammenhang gilt auch für das schwere und das elektrische Feld. Der Mond hat z.B. nur ca. 1/81 der Erdmasse. In einem Abstand von 3600 km vom Mondmittelpunkt, was dem Erdradius entspricht, ist daher auch die Kraftwirkung nur 1/81 der Erdanziehungskraft.
Die Stärke eines Feldes um einen geladenen Gegenstand ist proportional zu seiner Ladung:
[math]g \sim m \qquad E \sim Q \qquad H \sim Q_m [/math] "Doppelte Ladung --> Doppelte Feldstärke"
Feldfluß, Quellenstärke und Feldkonstanten
Die beiden Zusammenhänge zwischen Feldstärke und Flächeninhalt einerseits und Feldstärke und Ladung andererseits kann man nun zusammenfassen. Am Beispiel für das elektrische Feld:
- [math] E \, A \sim Q[/math]
Normalerweise fügt man nun an der rechten Seite der Gleichung eine Proportionalitätskonstante ein. Es hat sich aber eingebürgert, sie auf der linken Seite einzufügen.
- [math]\epsilon_0 \, E \, A = Q[/math]
Die sogenannte "elektrische Feldkonstante" [math]\epsilon_0[/math] beschreibt, wie die Einheiten der drei Größen zusammenhängen: Bei einer Feldstärke von 1 N/C und einer Oberfläche von 1m^2 beträgt die von der Fläche umschloßene Ladung [math]8{,}85 \cdot 10^{-12} \textstyle C[/math].
Dies ist nun die Präzisierung, die wir gesucht haben! Anstatt zu sagen, dass die Feldlinien dicht liegen beschreiben wir das mit einem großen Feldfluß durch die Fläche. Den Fluß des elektrischen Feldes legen wir als [math]\epsilon_0 \, E \, A[/math] fest.
Für schwere und magnetische Felder läßt sich das Ergebnis ebenso zusammenfassen:
Der Fluß[1]eines Feldes durch eine Feldfläche entspricht der von der Fläche umschlossenen Ladung: [math] \frac{1}{4\pi \,G} \ g \, A = m \qquad \epsilon_0 \, E \, A = Q \qquad \mu_0 \, H \, A = Q_m[/math]
Quellenstärke und Feldfluß für beliebige Felder
Verallgemeinerung auf beliebige Ladungsverteilungen und beliebige geschlossene Flächen.
Felderzeugende Ladung und Feldstärke (Erste Maxwellsche Gleichung)
Die Ergebnisse des Cavendish-Experimens lassen sich auf zwei Weisen anwenden:
- Man kann bei bekannter Ladungsmenge die mittlere Feldstärke durch eine Fläche bestimmen.
- Man kann bei bekannter mittlerer Feldstärke durch eine geschlossene Fläche auf die Ladung innerhalb der Fläche rückschließen.
Waren die Flächen beim Cavendish-Experiment Kugelschalen, so läßt sich das verallgemeinern:
- Man kann beliebige Äquipotentialflächen verwenden.
- Man kann sogar beliebige, geschlossene Flächen verwenden.
- Bei einer nicht konstanten Feldstärke rechnet man mit der mittleren Feldstärke [math]\bar E[/math].
- [math]Q = \epsilon_0 \, \bar E \, A[/math]
Auf diese elegant formulierte Art wird eindrücklich klar, dass die Ladungen Quellen und Senken des elektrischen Feldes sind. Es ist eine verallgemeinerte Version der Feldstärke des Zentralfeldes.
Allgemeine Beispiele
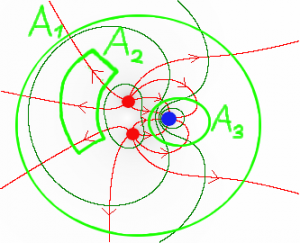
Die umschlossene Ladungsmenge und die mittlere Feldstärke durch die gewählte Fläche hängen direkt zusammen. Je nach Wahl der Fläche lassen sich verschiedene Aussagen machen.
A1: Die mittlere Feldstärke entspricht einer positiven Ladung.
A2: Die mittlere Feldstärke ist Null, die Fläche enthält keine Ladung.
A3: Die mittlere Feldstärke enstpricht einer negativen Ladung.
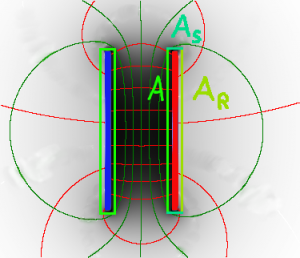
Anwendung beim Kondensator
Legt man um die positiv geladene Platte die Fläche A1, so laufen die Feldlinien aus der Fläche heraus, die enthaltene Ladung ist positiv. Bei A2 laufen die Feldlinien herein, die Ladung ist negativ.
Quantitativ erhält man den bereits bekannten Zusammenhang zwischen der Kondensatorfläche, der Feldstärke und der Ladung. Die Feldstärke ausserhalb des Kondensators kann man vernachlässigen.
Man erhält bei A1:
- [math]A_K[/math]: Kondensatorfläche
- [math]E_K[/math]: Feldstärke im Kondensator
- [math]Q=\varepsilon_0 \, E \, A = \varepsilon_0 \, \frac{1}{2}E_K \, 2 A_K[/math]
- [math]Q= \varepsilon_0 \, E_K \, A_K[/math]
Feld eines geladenen langen Drahtes (Zylinderfeld)
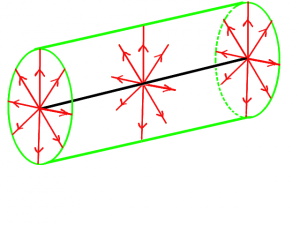
Denkt man sich den Cavendish-Versuch für einen langen, geladenen Draht, so läßt sich seine Feldstärke bestimmen.
Der Draht habe die Länge l und sei mit der Ladung Q geladen.
Man legt eine Zylinderfläche um den Draht, die aus Symmetriegründen auch Äquipotentialfläche ist. Die kreisförmigen Abschlüsse des Zylinders vernachlässigt man, weil man von einem relativ langen Draht ausgeht und die Flächen somit im Vergleich zur Mantelfläche sehr klein sind. Das elektrische Feld durch diese Flächen "ist Null".
Nun gilt:
- [math]A=2\pi \, r \, l[/math] (Mantelfläche des Zylinders)
- [math]E=\frac{1}{\varepsilon_0} \, \frac{Q}{A} = \frac{1}{\varepsilon_0} \, \frac{Q}{2\pi r l}[/math]
- [math]E=\frac{1}{\varepsilon_0 2\pi \, l} \, \frac{Q}{r}[/math]
Die Feldstärke nimmt also nur proportional zu [math]\frac{1}{r}[/math] ab und nicht wie beim Zentralfeld proportional zu [math] \frac{1}{r^2}[/math]!
Man sagt, das Feld hat eine größere Reichweite.
Für das Potential ergibt sich eine interessante Folgerung. Da es die Aufleitung (Stammfunktion) der Feldstärke ist, hat das Potential die Form:
- [math]\varphi(r)=\mathrm{c} \cdot \ln(r) [/math]
Beim Gravitationsfeld der Erde kann man für einen Körper eine Fluchtenergie bestimmen, mit der er das Feld der Erde langfristig verlässt. Aus dem logarithmischen Potential kann man ließen, dass eine Ladung mit einer gewissen Anfangsenegie dem Feld des geraden Leiters nicht entkommen kann. Auch so kann man den Begriff "größere Reichweite" interpretieren.
Fußnoten
- ↑ 1,0 1,1 Der Fluß der Feldstärke ist eigentlich nur [math]g\, A[/math] oder [math]E\, A[/math] oder [math]H\, A[/math], also das Produkt aus Feldstärke und Fläche. Damit ist die Feldstärke identisch mit der Flußdichte eines Feldes. Aber in der Physik hat sich für [math]\epsilon_0 \,E \, A[/math] und [math]\mu_0 \,H \, A[/math] der Begriff des elektrischen bzw. des magnetischen Flußes eingebürgert. Das ist eine der vielen Stolperfallen in den Bezeichnungen, die sich historisch so entwickelt haben.