Untersuchung von Schwingungen mit der Differentialgleichung: Unterschied zwischen den Versionen
(→Das Fadenpendel) |
K (→DGL) |
||
| Zeile 18: | Zeile 18: | ||
:<math>m\, \ddot y = - D \, y \quad \Leftrightarrow \quad \ddot y = -\frac{D}{m}\quad .</math> mit <math> .\quad D = 2\, A\, \varrho \, g</math> | :<math>m\, \ddot y = - D \, y \quad \Leftrightarrow \quad \ddot y = -\frac{D}{m}\quad .</math> mit <math> .\quad D = 2\, A\, \varrho \, g</math> | ||
| − | :<math>y(t)=\hat y \, \sin(\omega \, t) \ | + | :<math>y(t)=\hat y \, \sin(\omega \, t) \qquad .</math> mit <math>.\quad \omega^2 = \frac{D}{m}</math> |
Dabei ist <math>m</math> die Masse der gesamten Flüssigkeit. | Dabei ist <math>m</math> die Masse der gesamten Flüssigkeit. | ||
| Zeile 30: | Zeile 30: | ||
Die Unabhängigkeit von der Masse kann man auch gut durch eine fiktive Teilung des U-Rohrs einsehen: Denkt man sich das Rohr parallel zur Zeichenebene halbiert, so erhält man zwei U-Rohre mit halbkreisförmigen Querschnitt. In jeder dieser Hälften schwingt die Flüssigkeit so wie vorher! | Die Unabhängigkeit von der Masse kann man auch gut durch eine fiktive Teilung des U-Rohrs einsehen: Denkt man sich das Rohr parallel zur Zeichenebene halbiert, so erhält man zwei U-Rohre mit halbkreisförmigen Querschnitt. In jeder dieser Hälften schwingt die Flüssigkeit so wie vorher! | ||
| − | <br style="clear: both" /> | + | <br style="clear: both" /> |
| − | + | ||
| − | + | ||
==Das Fadenpendel== | ==Das Fadenpendel== | ||
Version vom 9. Januar 2012, 22:32 Uhr
Inhaltsverzeichnis
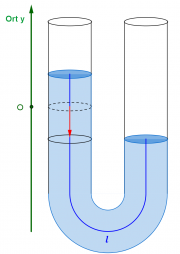
Schwingende Flüssigkeit im U-Rohr
Koordinatensystem
Den Ort der Flüssigkeit kann man durch die Lage eines Wasserspiegels beschreiben. Dabei sind Auslenkungen nach oben positiv und der Koordinatenursprung ist in der Ruhelage.
Kraftverlauf
Die Rückstellkraft entspricht der Gewichtskraft der Wassermenge, die sich über dem tieferen Wasserspiegel befindet. Die Masse läßt sich über das Volumen [math]V[/math] und die Dichte [math]\varrho[/math] der Flüssigkeit bestimmen. Das Volumen über die Querschnittsfläche [math]A[/math] und die Höhe [math]2\, y[/math]. Dabei ist die Höhe gerade die doppelte Auslenkung der Wassersäule!
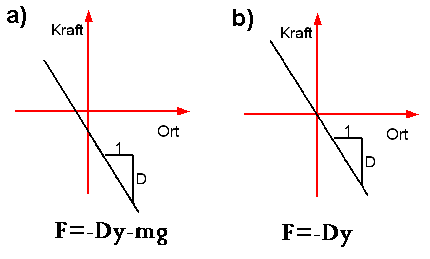
- [math]F = - m_y\, g = -\, V\, \varrho \, g = -\, A\, 2\, y\, \varrho \, g = -(2\, A\, \varrho \, g)\, y[/math]
Die Rückstellkraft ist also proportional zur Auslenkung, die Schwingung ist harmonisch!
DGL
Der Proportionalitätsfaktor [math]2\, A\, \varrho \, g[/math] entspricht der Federkonstanten [math]D[/math]. Daraus folgt direkt die Differentialgleichung und deren Lösung:
- [math]m\, \ddot y = - D \, y \quad \Leftrightarrow \quad \ddot y = -\frac{D}{m}\quad .[/math] mit [math] .\quad D = 2\, A\, \varrho \, g[/math]
- [math]y(t)=\hat y \, \sin(\omega \, t) \qquad .[/math] mit [math].\quad \omega^2 = \frac{D}{m}[/math]
Dabei ist [math]m[/math] die Masse der gesamten Flüssigkeit.
Es sieht also zunächst so aus, als ob die Frequenz von der Dichte der Flüssigkeit und auch von der Dicke des Rohres abhängt. Aber die Masse der schwingenden Flüssigkeit hängt auch von der Querschnittsfläche und von der Dichte ab! Man kann man die Form der Flüssigkeit als einen "gebogenen Zylinder" ansehen, der näherungsweise das gleiche Volumen hat wie der gerade Zylinder. Die Länge des Zylinders wird [math]l[/math] genannt:
- [math]\omega^2 = \frac{D}{m} = \frac{2\, A\, \varrho \, g}{V\, \varrho } = \frac{2\, A\, \varrho \, g}{A \, l\, \varrho } = \frac{2\, g}{l}[/math]
Die Frequenz hängt also nicht von der Masse oder der Dichte der schwingenden Flüssigkeit ab!
Die Unabhängigkeit von der Masse kann man auch gut durch eine fiktive Teilung des U-Rohrs einsehen: Denkt man sich das Rohr parallel zur Zeichenebene halbiert, so erhält man zwei U-Rohre mit halbkreisförmigen Querschnitt. In jeder dieser Hälften schwingt die Flüssigkeit so wie vorher!
Das Fadenpendel
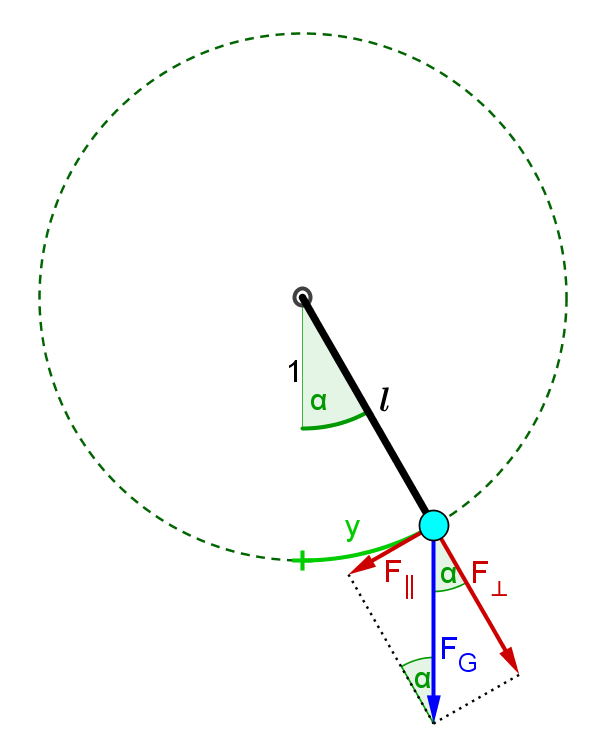
Koordinatensystem
Am geeignetsten ist ein gebogenes System, das genau dem Weg des Pendelkörpers folgt. Die Ruhelage ist der Ursprung und Ausschläge nach rechts sind positiv.
Der Ort auf dem Kreis hängt direkt mit dem Winkel (im Bogenmaß) zusammen:
- [math]y = l\, \varphi\quad \Leftrightarrow \quad \varphi = \frac{y}{l}[/math]
Kraftverlauf
Die Rückstellkraft kommt durch durch die Gewichtskraft des Pendelkörpers zustande. Sie muss parallel zur Bewegungsrichtung wirken, das heißt die Rückstellkraft ist der zur Bewegungsrichtung parallele Anteil der Gewichtskraft:
- [math]F(y) = - \, F_g \, \sin(\varphi) = - \, m\, g \, \sin(\frac{y}{l})[/math]
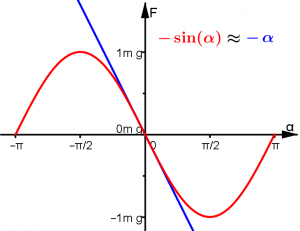
Die Rückstellkraft ist also nicht proportional zur Auslenkung und die Schwingung ist nicht harmonisch! An der graphischen Darstellung des Kraftverlaufs sieht man gut, dass man bei einem Winkel von 90° die maximale Rückstellkraft, nämlich gerade die gesamte Gewichtskraft erreicht hat. Für Werte über 90°, die man mit einer Stange als Befestigung auch erreichen kann, nimmt die Rückstellkraft dann für größere Winkel wieder ab.
Man kann den Kraftverlauf für kleine Ausschläge linear nähern, indem man die Sinuskurve durch die Tangente an der Stelle [math]y=0[/math] ersetzt. Die Steigung beträgt dort:
- [math]F'(y)= - \, m\, g \, \frac{1}{l}\, \sin(\frac{y}{l})\quad \Rightarrow \quad F'(0) = - \, m\, g \, \frac{1}{l}[/math]
Demnach gilt für den Kraftverlauf ungefähr:
- [math]F(y)\approx - \, \frac{m \, g}{l} \, y[/math]
Differentialgleichung
Für die lineare Näherung ergibt sich die DGL einer harmonischen Schwingung:
- [math]\ddot y = - \, \frac{D}{m}\,y = - \, \frac{m\, g}{l\, m}\, y = - \, \frac{g}{l}\, y[/math]
und die bekannten Lösungen
- [math]y(t) = \hat y \, \sin(\omega \, t)[/math] mit [math]\omega ^2 = \frac{g}{l}[/math]