Aufgaben zu den Grundlagen über Felder (Lösungen): Unterschied zwischen den Versionen
K (→Graphische Darstellung von Feldern) |
(→Potential) |
||
| (51 dazwischenliegende Versionen des gleichen Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | ([[Inhalt_Kursstufe|'''Kursstufe''']] > [[Inhalt_Kursstufe#Grundlagen elektrischer, magnetischer und schwerer Felder|'''Grundlagen elektrischer, magnetischer und schwerer Felder''']]) | |
| − | + | ||
| − | + | *[[Aufgaben zu den Grundlagen über Felder|'''Zurück zu den Aufgaben''']] | |
==Fern- und Nahwirkungstheorie== | ==Fern- und Nahwirkungstheorie== | ||
| − | + | ;1) Das Feld als Vermittler einer Wechselwirkung | |
| + | *Zwischen den Gegenständen, die miteinander wechselwirken, befindet sich ein elektrisches, magnetisches oder gravitatives Feld. Das Feld vermittelt die Wechselwirkung. | ||
| + | *Ein Feld kann sich nur mit einer endlichen Ausbreitungsgeschwindigkeit verändern und es kann Energie speichern. | ||
| − | |||
| − | + | ;2) Formulierungen und Übersetzungen | |
| + | :a) Fernwirkungstheorie: Sonne und Erde ziehen sich an. | ||
| + | :b) Probekörper im Feld: Die Kompassnadel richtet sich im Erdmagnetfeld aus. | ||
| + | :c) Fernwirkungstheorie: Der geriebene Luftballon zieht die Papierschnipsel an. | ||
| + | :d) aktives Feld: Apfel und Erde werden zueinandergezogen. | ||
| + | :e) Fernwirkungstheorie: Die positiv geladene Kugel und die negativ geladene Kugel ziehen sich an. | ||
| + | :f) aktives Feld: Das Magnetfeld zwischen Nord- und Südpol zieht die beiden Pole aufeinander zu. | ||
| − | * | + | * Formuliere die obigen Aussagen in allen drei Theorien. |
| − | + | :''Fernwirkungstheorie'' | |
| + | :a) Sonne und Erde ziehen sich an. | ||
| + | :b) Der Nordpol des Kompasses und der magnetische Südpol der Erde ziehen sich an. | ||
| + | :c) Der geriebene Luftballon und die Papierschnipsel ziehen sich an. | ||
| + | :d) Apfel und Erde ziehen sich an. | ||
| + | :e) Die positiv geladene Kugel und die negativ geladene Kugel ziehen sich an. | ||
| + | :f) Nord- und Südpol ziehen sich an. | ||
| − | + | :''Nahwirkungstheorie: Probekörper im Feld'' | |
| − | + | :a) Im Gravitationsfeld der Sonne wird die Erde zur Sonne gezogen. | |
| + | :b) Die Kompassnadel richtet sich im Erdmagnetfeld aus. | ||
| + | :c) Im elektrischen Feld des geriebenen Luftballons werden die Papierschnipsel zum Ballon gezogen. | ||
| + | :d) Der Apfel wird im Gravitationsfeld der Erde in Richtung Erde gezogen. | ||
| + | :e) Im elektrischen Feld der positiv geladenen Kugel erfährt die negativ geladene Kugel eine Kraftwirkung. (oder umgekehrt) | ||
| + | :f) Im Magnetfeld des Nordpols wird der Südpol in Richtung Nordpol gezogen. | ||
| − | + | :''Nahwirkungstheorie: aktives Feld'' | |
| + | :a) Das Gravitationsfeld zieht Sonne und Erde zueinander. | ||
| + | :b) Das Magnetfeld richtet die Kompassnadel nach Norden aus. | ||
| + | :c) Das elektrische Feld zieht den geriebenen Luftballon und die Papierschnipsel zusammen. | ||
| + | :d) Das Gravitationsfeld zieht Erde und Apfel zueinander. | ||
| + | :e) Das elektrische Feld zwischen der positiv geladenen Kugel und der negativ geladenen Kugel zieht die beiden zusammen. | ||
| + | :f) Das Magnetfeld zwischen dem Nord- und dem Südpol zieht die beiden zusammen. | ||
| − | + | ==Feldenergie== | |
| + | Begründen Sie möglichst anschaulich, warum ein Feld Energie enthält, indem Sie Beispiele nennen, bei denen Energie ins Feld gesteckt oder herausgeholt wird. | ||
| + | :Wenn der Nord und der Südpol zweier Magnete "zusammenkleben" und man sie voneinander trennt, so ist dazu Energie nötig. Ebenso, wenn man eine Tasche weiter von der Erde entfernt, sie also hochhebt. Wenn man annimmt, dass sich der Magnet und die Tasche dadurch nicht verändert haben, ist es sinnvoll anzunehmen, dass die Energie nun im Feld steckt. | ||
==Graphische Darstellung von Feldern== | ==Graphische Darstellung von Feldern== | ||
| + | ;1) Drei einfache Beispiele | ||
| + | *Zeichnen Sie einige Feldlinien mit Pfeilen (rot) und Feldflächen (grün) ein. | ||
{| | {| | ||
| − | | | + | |style="vertical-align:top;"| |
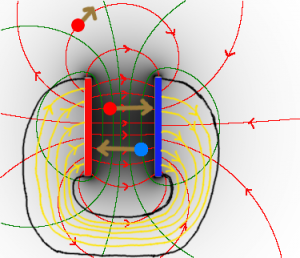
| − | a) geladene Kugel [[Datei: | + | a) geladene Kugel [[Datei:Aufgabe_Felder_Zeichnen_Zentralfeld_mit_Probekörper.png|300px]] |
| − | | | + | * |
| + | *Die positiv geladenen Probekörper (rot) werden in Richtung der Feldlinien gezogen, die negativen (blau) in die entgegengesetzte Richtung. | ||
| + | :Je geringer der Abstand, desto größer die Kraftwirkung. | ||
| + | |style="vertical-align:top;"| | ||
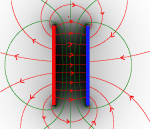
b) Ringmagnet | b) Ringmagnet | ||
| − | [[Datei: | + | [[Datei:Aufgabe_Felder_Zeichnen_Ringmagnet_Lösung.png|300px]] |
| − | | | + | *Das Magnetfeld zieht längs der Linien die Pole zusammen. |
| + | *Die Nordpole (rot) werden in Richtung der Feldlinien gezaogen, die Südpole (blau) in die entgegengesetzte Richtung. | ||
| + | |style="vertical-align:top;"| | ||
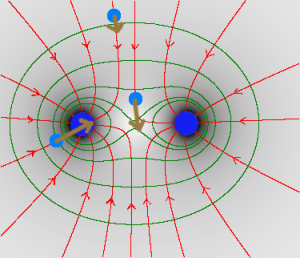
c) Zwei Sonnen | c) Zwei Sonnen | ||
| − | [[Datei: | + | [[Datei:Aufgabe_Felder_Zeichnen_Sonnen_Lösung.png|300px]] |
| + | *Das Gravitationsfeld zieht die beiden Sonnen längs der Feldflächen zueinander. | ||
| + | *Die Probemassen werden in Richtung der Feldlinien gezogen. | ||
|} | |} | ||
| + | ;2) und noch mehr Felder... | ||
| + | *Zeichnen Sie das Feld folgender Situationen. | ||
| + | :Erklären Sie jeweils mit Hilfe von Druck und Zugspannungen, wie das Feld zieht und drückt. | ||
| − | + | <gallery widths=150px heights=130px perrow=4 > | |
| − | + | Bild:Magnetfeld Darstellung Stabmagnet sw Linien Flächen Pole.png|Ein langer Stabmagnet. Das Feld zieht die Pole aufeinander zu. | |
| + | Bild:Felder Kondensator Stabmagnet nah.png|Ein Scheibenmagnet. Gleiche Zugspannung wie beim längeren Stabmagneten. | ||
| + | Bild:Feld Probekörper positiv.jpg|Eine "kleine" positve Ladung in einem homogenen Feld. Die Ladung wird vom Feld nach rechts gezogen. | ||
| + | Bild:Drei_Stabmagnete_sw_Linien_Pfeile_Flächen.png|Drei Stabmagnete aneinandergereiht. | ||
| + | Bild:Felder minus minus ungleich.png|Erde und Mond | ||
| + | Bild:Felder plus minus großer Abstand sw Linien Flächen.png|Ein Dipol mit großem... | ||
| + | Bild:Felder plus minus kleiner Abstand sw Linien Flächen.png|und mit kleinem Abstand. | ||
| + | Bild:Felder plus minus ungleich sw Linien Flächen.png|Ein Dipol mit ungleicher Ladungsverteilung. Aus größerer Entfernung entspricht das Feld dem eines positiv geladenen Gegenstandes. | ||
| + | </gallery> | ||
| − | == | + | ==Feldstärke== |
| − | + | ;1) Gravitation auf der Erde und auf anderen Himmelskörpern | |
| − | + | :a) Das Gravitationsfeld zieht die Erde und ein Kilogramm Masse mit einer Kraft von ca. 10 Newton aufeinander zu. Die Gravitationsfeldstärke beträgt daher 10 Newton pro Kilogramm: <math>g=\frac{F}{m} = 10\,\rm \frac{N}{kg}</math> | |
| + | :b)Ich habe eine Masse von ca. 80kg. Meine Gewichtskraft beträgt daher auf dem Mond: | ||
| + | ::<math>F= m\, g = 80\,\rm kg \cdot 1{,}62\,\rm \frac{N}{kg} = 129{,}6\, N</math> | ||
| + | :c) Die vollständige Tabelle: | ||
| + | ::{|class="wikitable" style="text-align: center; " | ||
| + | !style="border-style: solid; border-width: 5px "| | ||
| + | Planet | ||
| + | !valign="top"; style="border-style: solid; border-width: 5px "| | ||
| + | Feldstärke(N/kg) | ||
| − | + | !valign="top"; style="border-style: solid; border-width: 5px "| | |
| + | Masse(kg) | ||
| − | + | !valign="top"; style="border-style: solid; border-width: 5px "| | |
| + | Kraft(N) | ||
| − | = | + | |- |
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | Merkur | ||
| − | == | + | |style="border-style: solid; border-width: 5px "| |
| + | 3,70 | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 80 | ||
| − | + | |style="border-style: solid; border-width: 5px "| | |
| + | 296 | ||
| − | + | |- | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | Venus | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 8,87 | ||
| − | = | + | |style="border-style: solid; border-width: 5px "| |
| + | 75 | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 665 | ||
| + | |- | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | Erde | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 9,77 | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 12,7 | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 124 | ||
| + | |- | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | Mars | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 3,69 | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 1000 | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 3690 | ||
| + | |- | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | Jupiter | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 23 | ||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 75 | ||
| + | |||
| + | |style="border-style: solid; border-width: 5px "| | ||
| + | 1725 | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | ;2) Kraftwirkung im elektrischen Feld | ||
| + | :Die elektrische Feldstärke ist als Ortsfaktor, also als Kraft pro Ladung, definiert: | ||
| + | <math> | ||
| + | \begin{array}{rrcl} | ||
| + | & E & = & \frac{F}{Q} \\ | ||
| + | \Rightarrow & F & = & Q\, E = 5\cdot 10^{-9}\,\rm C \cdot 10000\,\rm \frac{N}{C} = 5\cdot 10^{-5}\, N = 0{,}05\, mN | ||
| + | \end{array} | ||
| + | </math> | ||
| + | <br style="clear: both" /> | ||
| + | |||
| + | ;3) Berechnung der magnetischen Ladung | ||
| + | :Auch die magnetische Feldstärke ist als Ortsfaktor, als Kraft pro magnetische Ladung, definiert: | ||
| + | <math> | ||
| + | \begin{array}{rrcl} | ||
| + | & H & = & \frac{F}{Q_m} \\ | ||
| + | \Rightarrow & Q_m & = & \frac{F}{H} = \frac{0{,}5\,\rm N}{80000\,\rm\frac{N}{Wb}} = 6{,}3 \cdot 10^{-6}\,\rm Wb = 0{,}0063\, mWb | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | ;4) Definition der Feldstärke | ||
| + | :Die Feldstärke soll eine Aussage über das Feld machen, die unabhängig von der Art des Probekörpers ist. Wegen der Proportionalität zwischen Ladung (Masse) und Kraftwirkung ist die Kraft pro Ladung (Masse) an einer Stelle des Feldes konstant. Dieser Quotient aus Kraft und Ladung (Masse) ist also eine Eigenschaft des Feldes an dieser Stelle. | ||
| + | |||
| + | :Zur Messung der Feldstärke als Kraft pro Ladung muß man die Ladung (oder Masse) und die Kraft messen. | ||
| + | :Ein Coulomb elektrische Ladung ist mit Hilfe von elektrischen Strömen festgelegt worden, als die Ladung, welche in einer Sekunde bei einem Strom der Stärke ein Ampère fließt. Man kann die elektrische Ladung deshalb mit einem Stromstärkemessgerät und einer Uhr messen. (In der Praxis verwendet man einen geeigneten Messverstärker.) Die Masse von einem Kilogramm ist durch das [[Massenträgheit;_die_träge_Masse#Definition_der_Masse|Standardkilogramm]] in Paris festgelegt und Massen kann man ganz einfach mit einer Waage messen. | ||
| + | :Für die magnetische Ladung gibt es kein übliches Messgerät. Man könnte zwar eines bauen, aber es wäre recht umständlich.<ref>Siehe auch [[Die magnetische Feldstärke]] und [[Messung der magnetischen Ladung (4st)]].</ref> | ||
| + | |||
| + | |||
| + | ;5) Tischtennisball im geladenen Kondensator | ||
| + | [[Datei:Aufgabe_Ball_im_Kondensator_Vektorzeichnung.png|thumb]] | ||
| + | :Die Summe der elektrischen Kraft und der Gewichtskraft muss genau in Richtung des Fadens ziehen. Daraus folgt: | ||
| + | :<math> | ||
| + | \begin{array}{rrcl} | ||
| + | & \frac{F_e}{F_g} & = & \tan 4^\circ \\ | ||
| + | \Rightarrow & F_e & = & \tan 4^\circ \, m\, g = 0{,}0699 \cdot 0{,}0023\,\rm kg \cdot 10\frac{N}{kg} = 0{,}0699 \cdot 0{,}023\,\rm N = 1{,}6\, mN | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | Aus der bekannten Feldstärke und der elekrischen Feldkraft kann man nun die Ladung berechnen: | ||
| + | :<math> | ||
| + | \begin{array}{rrcl} | ||
| + | & E & = &\frac{F_e}{Q} & | \cdot Q \\ | ||
| + | \Rightarrow & Q\, E & = & F_e & | \mathopen: E \\ | ||
| + | \Rightarrow & Q & = & \frac{F_e}{E}& \\ | ||
| + | & & = & \frac{1{,}6\cdot 10^{-3}\,\rm N}{10^{5}\,\rm\frac{N}{C}}& = 16\cdot 10^{-9}\,\rm C = 16\,\rm nC \\ | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | ;6) Das elektrische Feld der Erde | ||
| + | :Die Summe von elektrischer Kraft und Gewichtskraft muss gerade Null sein, dass heißt die Kräfte sind betragsmäßig gleich groß: | ||
| + | <math>\begin{array}{rrcl} | ||
| + | &F_e &=& F_g \\ | ||
| + | &Q\, E &=& m\, g \\ | ||
| + | \Rightarrow & Q &=& \frac{m\, g}{E} | ||
| + | \end{array}</math> | ||
| + | :Bei wolkenlosen Himmel: | ||
| + | ::<math>Q = \frac{1\cdot 10^{-6}\,\rm kg \, 10\rm\frac{N}{kg}}{200\,\rm\frac{N}{C}} = 50\,\rm nC</math> | ||
| + | :Bei Gewitter: | ||
| + | ::<math>Q = \frac{1\cdot 10^{-6}\,\rm kg \, 10\rm\frac{N}{kg}}{30000\,\rm\frac{N}{C}} = 0{,}33\,\rm nC</math> | ||
| + | |||
| + | ==Potential== | ||
| + | ;1) Potentialunterschiede am Schauinsland | ||
| + | :Der Schauinsland im Schwarzwald hat eine Höhe von 1284 ü NHN, die Stadt Freiburg liegt am Fuße des Schauinslands auf 278 ü NHN. | ||
| + | :a) Wieviel Energie benötigt man, um eine Wasserflasche mit 1kg Masse (einen Rucksack mit 15kg Masse) von Freiburg auf den Schauinsland zu bringen? | ||
| + | :Bei einem Höhenunterschied h berechnet sich die potentielle Energie als | ||
| + | ::<math>E_{pot}=m\,g h = 1\,\rm kg \cdot 9{,}81\,{\rm \frac{N}{kg}}\cdot (1284\,\rm m - 278\,\rm m) = 1\,\rm kg \cdot 9{,}81\,{\rm \frac{N}{kg}}\cdot 1006\,\rm m = 9869 \,\rm Nm = 9{,}869 \,\rm kJ</math> | ||
| + | :Für den Rucksack benötigt man die 15-fache Energiemenge, weil die potentielle Energie proportional zur Masse ist: | ||
| + | ::<math>E_{pot}=m\,g h = 15\cdot 9{,}869 \,\rm kJ = 14{,}8 \,\rm kJ</math> | ||
| + | :b) Wie groß ist die Potentialdifferenz zwischen Freiburg und dem Schauinsland? | ||
| + | :Die Potentialdifferenz gibt den Unterschied der potentiellen Energie pro kg an. Und genau die hat man bereits ausgerechnet, sie beträgt <math>9{,}869 \,\rm{\frac{kJ}{kg}} </math> | ||
| + | :c) Das Nullniveau der potentiellen Energie soll auf Meereshöhe liegen. Berechne das Potential des Gravitationsfeldes für Freiburg und den Schauinslandgipfel. | ||
| + | :Das Potential gibt die potentielle Energie pro Masse an: | ||
| + | ::Potential für Freiburg: <math>\varphi = \frac{E_{pot}}{m} = \frac{m\, g h}{m} = gh = 9{,}81\,{\rm \frac{N}{kg}}\cdot 278\,\rm m = 2727\,{\rm \frac{Nm}{kg}} = 2727\,{\rm \frac{J}{kg}}</math> | ||
| + | ::Potential für den Schauinsland: <math>\varphi = gh = 9{,}81\,{\rm \frac{N}{kg}}\cdot 1284\,\rm m = 12596\,{\rm \frac{Nm}{kg}} = 12596\,{\rm \frac{J}{kg}}</math> | ||
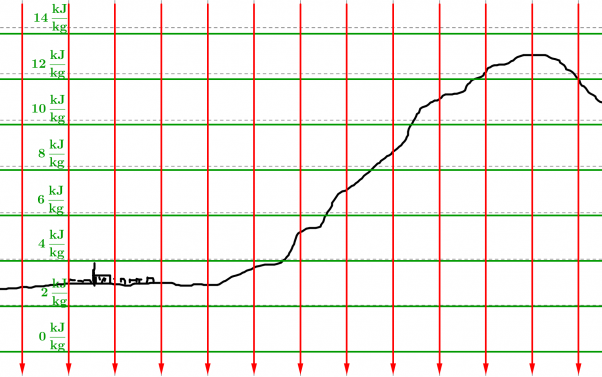
| + | :d) Zeichne das Gravitationsfeld oberhalb von Freiburg mit Hilfe einiger Feldlinien und den Potentialflächen von 0J/kg, 2000J/kg, 4000J/kg, ... , 14000J/kg. | ||
| + | ::[[Datei:Aufgabe_Potential_Schauinsland_Lösung.png|602px]] | ||
| + | |||
| + | ;2) Ein Plattenkondensator | ||
| + | :Die beiden Platten eines Kondensators werden an eine Hochspannungsquelle von 10kV angeschlossen. Die Platten sind 20 cm x 20 cm groß und 5cm voneinander entfernt. Der Einfachheit halber gehen wir davon aus, dass sich nur zwischen den Platten ein elektrisches Feld befindet, welches deshalb auch homogen ist. | ||
| + | :a,b,e) [[Datei:Aufgabe_Potential_Kondensator_Lösung.png|400px]] | ||
| + | :c) Wie groß ist die Stärke des elektrischen Feldes zwischen den Platten? | ||
| + | ::<math>E=\frac{\triangle\varphi}{\triangle s}=\rm \frac{10\, kV}{0{,}05\, m}=200000\frac{V}{m}=200000\frac{N}{C}</math> | ||
| + | :d) Ein Tischtennisball wird an einem sehr langen Faden in das Feld gehängt. Durch den langen Faden wird der Ball bei einer Auslenkung aus der Ruhelage kaum angehoben. Welche Art von Bewegung vollzieht er, wenn man ihn kurz mit der positiv geladenen Platte in Berührung bringt? | ||
| + | ::Der Ball wird immer schneller, er bekommt Energie aus dem Feld. Wegen der konstanten Feldstärke ist auch die beschleunigende Kraft konstant. Der Ball wird [[Gleichmäßig beschleunigte Bewegung mit konstanter Impulsänderung|gleichmäßig beschleunigt]]. | ||
| + | :e) Vergleichen Sie die Bewegung mit dem Rollen einer Kugel im Potential. | ||
| + | ::Im Modell rollt der Ball die schiefe Potentialebene hinunter. Die potentielle Energie sinkt, die kinetische Energie steigt an. | ||
| + | :f) Wieviel Energie würde ein mit +1C geladener Ball (ein Elektron) erfahren, dass sich von der positiven zur negativen Platte bewegt? | ||
| + | ::<math>\varphi=\frac{W}{Q}</math> | ||
| + | ::<math>\Rightarrow W_{\rm Ball} = Q\,\varphi = \rm 1\, C \cdot 10\rm \frac{kJ}{C} = 10\,kJ</math> | ||
| + | ::<math>\Rightarrow W_e = Q\,\varphi = e\,\varphi \quad( = e\cdot 10\,\rm kV = 10\,\rm keV ) = \rm 1{,}6\cdot10^{-19} C \cdot 10\frac{kJ}{C} = 1{,}6\cdot 10^{-15} J</math> | ||
| + | :g) Wie schnell wäre er (das Elektron) an der negativen (positiven) Platte? | ||
| + | ::An der negativen Platte ist die gesamte potentielle Energie in kinetische Energie gewandelt worden: | ||
| + | ::<math>W_{\rm kin}=\frac{1}{2}\,m\,v^2</math> | ||
| + | ::<math>\Rightarrow v_{\rm Ball}=\sqrt{\frac{2\, W}{m}}= \sqrt{\frac{2\cdot 10\,\rm kJ}{0,002\,\rm kg}}=3160\rm \frac{m}{s}\approx 11400 \rm \frac{km}{h}</math> | ||
| + | ::Das ist unrealistisch schnell und liegt daran, dass man einen Tischtennisball normalerweise nur mit ca 10nC laden kann! | ||
| + | ::<math>\Rightarrow v_e=\sqrt{\frac{2\, W}{m}}= \sqrt{\frac{2\cdot 1{,}6\cdot 10^{-15} \rm J}{9{,}1\cdot 10^{-31}\rm kg}}= 59300000\frac{m}{s}</math> | ||
| + | ::Das Elektron kann in einer Vakuumröhre tatsächlich auf so eine hohe Geschwindigkeit beschleunigt werden! Das sind ca. 20% der Lichtgeschwindigkeit von 300000 km/s. | ||
| + | |||
| + | ;3) Eine Batterie | ||
| + | :Ein geladener Akku hat eine Spannung von 1,2V. Der Akku wird mit einem 2m langem Kabel kurzgeschlossen, wodurch das Kabel erwärmt wird. (Der Einfachheit halber nehmen wir an, dass die Spannung dabei zeitlich konstant ist.) | ||
| + | :a) Jedes Coulomb Ladung erhält 1,2 Joule Energie, das Elektron erhält also die Energiemenge: | ||
| + | ::<math>E_{pot}=Q \, \Delta \varphi = Q\, U = 1{,}6 \cdot 10^{-19} \mathrm{C} \cdot 1{,}2\, \rm V = 1{,}92 \cdot 10^{-19} \mathrm{J}</math> | ||
| + | :b) Die Feldstärke berechnet sich als Potentialänderung pro Strecke: | ||
| + | ::<math>E=\frac{\Delta \varphi}{\Delta s} = \frac{1{,}2\,\rm V}{2\,\rm m} = 0{,}6 \, {\rm \frac{V}{m}} = 0{,}6 \, {\rm \frac{N}{C}}</math> | ||
| + | :c) Die Kraft auf eine Ladung berechnet sich als Ladung mal Ortsfaktor: | ||
| + | ::<math>F=Q \, E = 1{,}6 \cdot 10^{-19} \mathrm{C} \cdot 0{,}6 \, {\rm \frac{N}{C}} = 0{,}96 \cdot 10^{-19} \mathrm{N}</math> | ||
| + | :d) Jedes Coulomb Ladung erhält 1,2 J Energie: | ||
| + | ::<math>E_{pot}= Q \, \Delta \varphi = Q\, U = 7200\,\rm C \cdot 1{,}2\,\rm V = 8640\,\rm J</math> | ||
| + | :(Das entspricht etwa dem Energiegehalt von 0,25ml Benzin.) | ||
| + | |||
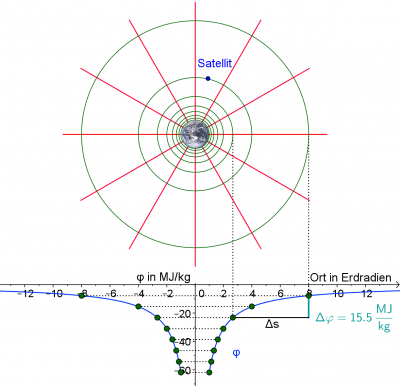
| + | ;4) Ein Satellit im Schwerefeld der Erde | ||
| + | :a) Wieviel Energie benötigt man, um den Satellit (Masse 800 kg) an die markierte Stelle zu heben? | ||
| + | :Das Potential steigt ungefähr von -62 MJ/kg auf -16 MJ/kg. Die Potentialdifferenz beträgt daher: | ||
| + | ::<math>\Delta \varphi = 46\,\rm \frac{MJ}{kg}</math> | ||
| + | :Der Zahlenwert gibt an, wieviel Energie man für ein Kilogramm Masse bräuchte. Für den Satelliten braucht man also die Energie: | ||
| + | ::<math>E_{pot} = m\,\rm \Delta \varphi = 500\,\rm kg \cdot 46\,\rm\frac{MJ}{kg} = 23000\,\rm MJ</math> | ||
| + | :(Das entspricht dem Energiegehalt von 800l Benzin!) | ||
| + | :b) Welche Kraft wirkt dort ungefähr auf ihn? | ||
| + | :Die Steigung des Potentials ist die Feldstärke, die man hier näherungsweise mit dem Differenzenquotienten bestimmt. (Man kann das in dieser [[Animation: Feldstärke und Potential des Gravitationsfeldes der Erde|Animation]] besser als im Bild ablesen.) | ||
| + | :Das Potential steigt im Abstand von ca. 2,5 Erdradien bis zu 8 Erdradien von ca. -24 MJ/kg auf -8MJ/kg: | ||
| + | :: <math>g = \varphi ' \approx \frac{\Delta \varphi}{\Delta s} \approx \frac{-8\,\rm \frac{MJ}{kg} - (-24\,\rm \frac{MJ}{kg})}{8\,r_E-2{,}5\,r_E} = \frac{16\,\rm \frac{MJ}{kg}}{6{,}5\,r_E} = \frac{16\cdot 10^{6}\rm \frac{J}{kg}}{6{,}5\cdot 6370 \cdot 10^{3}\,\rm m} \approx 0{,}39\,\rm \frac{N}{kg} </math> | ||
| + | :Die Feldstärke beträgt also dort nur noch ein Zwanzigstel der Feldstärke auf der Erde! | ||
| + | :Dementsprechend klein ist auch die "Gewichtskraft" auf den Satelliten: | ||
| + | ::<math>F = m\, g = 500\,\rm kg \cdot 0{,}39\,\rm \frac{N}{kg} =190\,\rm N</math> | ||
| + | |||
| + | {| | ||
| + | | | ||
| + | [[Datei:Aufgabe_Potential_Satellit_Lösung.png|400px]] | ||
| + | |valign="top"| | ||
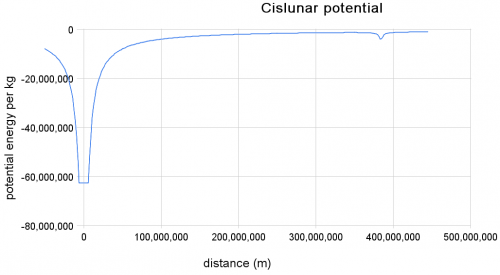
| + | [[Datei:Cislunar_potential.png|500px]] | ||
| + | |} | ||
| + | |||
| + | ;5) Mondstation | ||
| + | :a) Wieviel Energie benötigt man, damit man 1 Tonne Nachschub-Material auf eine Mondstation bringen kann? | ||
| + | :Um über den "Potentialberg" zu kommen, muß man die maximale Potentialdifferenz von <math>\Delta \varphi \approx 60\,\rm \frac{MJ}{kg}</math> überwinden. Danach geht es dann wieder ein wenig "bergab". | ||
| + | :Für eine Tonne Nachschub braucht man daher mindestens die Energie: | ||
| + | :<math>E_{pot} = m\,\Delta\,\varphi = 1000\,\rm kg \cdot 60\,\rm \frac{MJ}{kg} = 60.000 \,\rm MJ</math> | ||
| + | :b) Wieviel potentielle Energie hat das Material dann auf der Mondoberfläche? | ||
| + | :Weil es nach dem "Potentialberg" wieder ein wenig "bergab" ging, beträgt die Potentialdifferenz zur Erde nur ca. <math>\Delta \varphi \approx 58\,\rm \frac{MJ}{kg}</math>, die potentielle Energie beträgt also nur noch: | ||
| + | :<math>E_{pot} = m\,\Delta\,\varphi = 1000\,\rm kg \cdot 58\,\rm \frac{MJ}{kg} = 58.000 \,\rm MJ</math> | ||
| + | :c) Vergleichen Sie die Energiemengen mit Benzinmengen! (Ein Kilogramm Benzin enthält ca. 43 MJ Energie, ein Liter Benzin ca. 30 MJ.) | ||
| + | :Man braucht also mindestens 2000l oder 1,3t Benzin, um eine Tonne Nachschub auf den Mond zu bringen! (Man benötigt noch wesentlich mehr, denn für den Flug dorthin muss der Nachschub auch Bewegungsenergie bekommen, die man leider nicht mehr zurückgewinnen kann. Außerdem muss auch die gesamte Rakete mit dem Treibstoff hochgehoben und beschleunigt werden.) | ||
| + | |||
| + | ;6) Das Potential der Erde | ||
| + | Anton steht auf der Erde. Bertha befindet sich einen Erdradius oberhalb der Erdoberfläche in einer Raumkapsel. Cecilie ist zwei Erdradien von der Erde entfernt. (usw.) | ||
| + | :a) Berechnen Sie die Potentialunterschiede zwischen A und B, B und C, ... | ||
| + | :b) Berechnen Sie das Potential an den Stellen A, B, C, ... | ||
| + | |||
| + | ;7) Ein geostationärer Satellit | ||
| + | Ein Satellit (Masse 800 kg) soll in eine geostationäre Umlaufbahn, also in eine Höhe von etwa 36.000 km über der Erdoberfläche. Der Bahnradius beträgt dann ungefähr 42.000 km. | ||
| + | :a) Berechnen Sie mit Hilfe einer Gleichung für die Feldstärke oder des Potential die dazu nötige Energiemenge. | ||
| + | :b) Vergleichen Sie die Energiemengen mit Benzinmengen! (Ein Kilogramm Benzin enthält ca. 43 MJ Energie, ein Liter Benzin ca. 30 MJ.) | ||
| + | |||
| + | ==Schwere, Elektrische und Magnetische Wechselwirkung (Gravitation, Elektrostatik, Magnetostatik)== | ||
| + | Versuche beschreiben und erklären mit der Nahwirkungstheorie. | ||
| + | |||
| + | Segnersches Rad, "Wedelgenerator", ... | ||
| + | |||
| + | |||
| + | ==Ladung als Quellenstärke und der Fluss eines Feldes== | ||
===Masse der Erde=== | ===Masse der Erde=== | ||
| + | *Wieviel (schwere) Masse hat die Erde? | ||
| + | |||
Der Feldfluss durch die Erdoberfläche ist genauso groß wie die Erdmasse: | Der Feldfluss durch die Erdoberfläche ist genauso groß wie die Erdmasse: | ||
:<math>\frac{1}{4\pi \,G} \ g \, A = m</math> | :<math>\frac{1}{4\pi \,G} \ g \, A = m</math> | ||
| Zeile 70: | Zeile 332: | ||
Das ist schon ein recht vernünftiger Wert im Vergleich zu [http://de.wikipedia.org/wiki/Erdmasse genaueren Messwerten]. | Das ist schon ein recht vernünftiger Wert im Vergleich zu [http://de.wikipedia.org/wiki/Erdmasse genaueren Messwerten]. | ||
| − | |||
===Gravitationsfeldstärke im All=== | ===Gravitationsfeldstärke im All=== | ||
| − | *Wie groß ist die Gravitationsfeldstärke in einem Abstand von | + | *Wie groß ist die Gravitationsfeldstärke in einem Abstand von 6370 km über dem Erdboden? |
'''Mit Erdmasse''' | '''Mit Erdmasse''' | ||
| − | In einem Abstand von | + | In einem Abstand von 6370km über dem Erdboden ist man 12740km vom Ermittelpunkt entfernt. Man betrachtet den Feldfluss durch eine Kugeloberfläche mit diesem Radius. Dazu kann man die Formel für die Quellenstärke umformen: |
| − | :<math>g = 4 \pi \, G\, \frac{m}{A} = 4 \pi \ | + | :<math>g = 4 \pi \, G\, \frac{m}{A} = 4 \pi \cdot 6{,}67 \cdot 10^{-11} \mathrm{\frac{m^3}{kg \cdot s^2}} \cdot \frac{5{,}99 \cdot 10^{24}\rm kg}{4 \pi \, (12740000\,\rm m)^2} \approx 2{,}45 \,\rm \frac{N}{kg}</math> |
'''Verdopplung der Entfernung''' | '''Verdopplung der Entfernung''' | ||
| Zeile 85: | Zeile 346: | ||
Da der Fluss durch die Fläche aber gleich bleibt muss die Feldstärke auf ein Viertel abnehmen! | Da der Fluss durch die Fläche aber gleich bleibt muss die Feldstärke auf ein Viertel abnehmen! | ||
| − | :<math>g = \frac{1}{4} \ | + | :<math>g = \frac{1}{4} \cdot 9{,}81 \,{\rm\frac{N}{kg}} = 2{,}45 \,{\rm \frac{N}{kg}}</math> |
*Welche Kraft wirkt dort auf einen 1000kg schweren Satelliten? | *Welche Kraft wirkt dort auf einen 1000kg schweren Satelliten? | ||
Die Feldstärke ist der Ortsfaktor: | Die Feldstärke ist der Ortsfaktor: | ||
| − | :<math>g=\frac{F}{m} \qquad \Rightarrow \qquad F = m \, g = 1000 \rm kg \cdot 2{,}45 \frac{N}{kg} = 2450 \, N</math> | + | :<math>g=\frac{F}{m} \qquad \Rightarrow \qquad F = m \, g = 1000\, \rm kg \cdot 2{,}45 \frac{N}{kg} = 2450 \, N</math> |
| − | + | ||
===Gravitation in der Erdkugel=== | ===Gravitation in der Erdkugel=== | ||
| + | *Wie groß ist die Stärke des Schwerefeldes innerhalb der Erdkugel? | ||
[[Datei:Erde_mit_Innenkreis.png|thumb]] | [[Datei:Erde_mit_Innenkreis.png|thumb]] | ||
Man betrachtet eine Kugeloberfläche mit dem Radius r. Damit läßt sich die Feldstärke im Abstand r vom Erdmittelpunkt berechnen. | Man betrachtet eine Kugeloberfläche mit dem Radius r. Damit läßt sich die Feldstärke im Abstand r vom Erdmittelpunkt berechnen. | ||
| Zeile 98: | Zeile 359: | ||
Dazu nehmen wir vereinfachend an, dass die Erde überall die gleiche Massendichte <math>\rho</math> hat. | Dazu nehmen wir vereinfachend an, dass die Erde überall die gleiche Massendichte <math>\rho</math> hat. | ||
| − | Nun ist der Fluss aus der Fläche gleich der enthaltenen Masse. Die Masse | + | Nun ist der Fluss aus der Fläche gleich der enthaltenen Masse. Die Masse außerhalb der Kugel spielt keine Rolle! Das ist erstaunlich. Die Wirkung der Kugelschale außerhalb der Kugel hebt sich gerade auf. (Vgl. Wikipedia: [http://de.wikipedia.org/wiki/Kugelschale#Schwerelosigkeit_im_Innern_einer_Kugelschale Kugelschale].) |
:<math>\frac{1}{4 \pi \, G} \, g \, A = m \qquad \Rightarrow \qquad g = 4 \pi \, G \, \frac{m}{A} = 4 \pi \, G \, \frac{V \, \rho}{A}\qquad .</math>( mit <math>m= V\, \rho</math>) | :<math>\frac{1}{4 \pi \, G} \, g \, A = m \qquad \Rightarrow \qquad g = 4 \pi \, G \, \frac{m}{A} = 4 \pi \, G \, \frac{V \, \rho}{A}\qquad .</math>( mit <math>m= V\, \rho</math>) | ||
| Zeile 113: | Zeile 374: | ||
Zwei geladene Platten, je 30cm x 30cm groß, eine mit 8 10<sup>-8</sup> C, die andere mit -8 10<sup>-8</sup> C. | Zwei geladene Platten, je 30cm x 30cm groß, eine mit 8 10<sup>-8</sup> C, die andere mit -8 10<sup>-8</sup> C. | ||
| − | * | + | *Zur Berechnung der Feldstärke legt man eine Fläche um eine Platte ([[Ladung_als_Quellenstärke_und_der_Fluss_eines_Feldes#Homogenes Feld eines Kondensators / Ringmagneten|vgl. hier]]): |
| + | ::<math> E= \frac{1}{\epsilon_0} \, \frac{Q}{A} = \frac{1}{8{,}854 \cdot 10^{-12} \frac {\mathrm{A}\,\mathrm{s}} {\mathrm{V}\,\mathrm{m}} } \cdot \frac{8 \cdot 10^{-8}\,\rm C}{0{,}3\,\rm m\cdot 0{,}3\,\rm m} = \frac{1}{8{,}854 \cdot 10^{-12} \frac {\mathrm{A}\,\mathrm{s}} {\mathrm{V}\,\mathrm{m}} } \cdot 8{,}89 \cdot 10^{-7}\,{\rm\frac{C}{m^2}} = 100400\,{\rm \frac{V}{m}} </math> | ||
*Warum ist dabei die Feldstärke zwischen den Platten nicht vom Abstand der Platten abhängig? | *Warum ist dabei die Feldstärke zwischen den Platten nicht vom Abstand der Platten abhängig? | ||
| + | :Wenn man annimmt, dass sich nur zwischen den Platten elektrisches Feld befindet, dann hängt die Feldstärke nur von der Ladungsmenge pro Fläche, der Flächenladungsdichte ab. ([[Ladung als Quellenstärke und der Fluss eines Feldes#Homogenes Feld eines Kondensators / Ringmagneten| Eine genauere Erklärung steht hier.]]) | ||
| + | |||
Zwischen die Platten wird ein negativ geladener Tischtennisball gehängt. Auf ihn wirkt eine Kraft von 0,01 N. | Zwischen die Platten wird ein negativ geladener Tischtennisball gehängt. Auf ihn wirkt eine Kraft von 0,01 N. | ||
| − | * | + | *Der Ball wird in Richtung der positiv geladenen Platte gezogen. |
| − | * | + | *Aus der Feldstärke ergibt sich die Menge der Probeladung: |
| − | + | ::<math>E=\frac{F}{Q}\quad \Rightarrow \quad Q=\frac{F}{E} = \frac{0{,}01\,\rm N}{100400\,{\rm \frac{N}{C}}} = 10\cdot 10^{-8}\,\rm C = 100 \,\rm nC</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | : | + | |
| − | + | ||
| − | : | + | |
| − | + | ||
| − | === | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | = | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
==Fußnoten== | ==Fußnoten== | ||
<references /> | <references /> | ||
Aktuelle Version vom 18. Juli 2018, 07:40 Uhr
(Kursstufe > Grundlagen elektrischer, magnetischer und schwerer Felder)
Inhaltsverzeichnis
Fern- und Nahwirkungstheorie
- 1) Das Feld als Vermittler einer Wechselwirkung
- Zwischen den Gegenständen, die miteinander wechselwirken, befindet sich ein elektrisches, magnetisches oder gravitatives Feld. Das Feld vermittelt die Wechselwirkung.
- Ein Feld kann sich nur mit einer endlichen Ausbreitungsgeschwindigkeit verändern und es kann Energie speichern.
- 2) Formulierungen und Übersetzungen
- a) Fernwirkungstheorie: Sonne und Erde ziehen sich an.
- b) Probekörper im Feld: Die Kompassnadel richtet sich im Erdmagnetfeld aus.
- c) Fernwirkungstheorie: Der geriebene Luftballon zieht die Papierschnipsel an.
- d) aktives Feld: Apfel und Erde werden zueinandergezogen.
- e) Fernwirkungstheorie: Die positiv geladene Kugel und die negativ geladene Kugel ziehen sich an.
- f) aktives Feld: Das Magnetfeld zwischen Nord- und Südpol zieht die beiden Pole aufeinander zu.
- Formuliere die obigen Aussagen in allen drei Theorien.
- Fernwirkungstheorie
- a) Sonne und Erde ziehen sich an.
- b) Der Nordpol des Kompasses und der magnetische Südpol der Erde ziehen sich an.
- c) Der geriebene Luftballon und die Papierschnipsel ziehen sich an.
- d) Apfel und Erde ziehen sich an.
- e) Die positiv geladene Kugel und die negativ geladene Kugel ziehen sich an.
- f) Nord- und Südpol ziehen sich an.
- Nahwirkungstheorie: Probekörper im Feld
- a) Im Gravitationsfeld der Sonne wird die Erde zur Sonne gezogen.
- b) Die Kompassnadel richtet sich im Erdmagnetfeld aus.
- c) Im elektrischen Feld des geriebenen Luftballons werden die Papierschnipsel zum Ballon gezogen.
- d) Der Apfel wird im Gravitationsfeld der Erde in Richtung Erde gezogen.
- e) Im elektrischen Feld der positiv geladenen Kugel erfährt die negativ geladene Kugel eine Kraftwirkung. (oder umgekehrt)
- f) Im Magnetfeld des Nordpols wird der Südpol in Richtung Nordpol gezogen.
- Nahwirkungstheorie: aktives Feld
- a) Das Gravitationsfeld zieht Sonne und Erde zueinander.
- b) Das Magnetfeld richtet die Kompassnadel nach Norden aus.
- c) Das elektrische Feld zieht den geriebenen Luftballon und die Papierschnipsel zusammen.
- d) Das Gravitationsfeld zieht Erde und Apfel zueinander.
- e) Das elektrische Feld zwischen der positiv geladenen Kugel und der negativ geladenen Kugel zieht die beiden zusammen.
- f) Das Magnetfeld zwischen dem Nord- und dem Südpol zieht die beiden zusammen.
Feldenergie
Begründen Sie möglichst anschaulich, warum ein Feld Energie enthält, indem Sie Beispiele nennen, bei denen Energie ins Feld gesteckt oder herausgeholt wird.
- Wenn der Nord und der Südpol zweier Magnete "zusammenkleben" und man sie voneinander trennt, so ist dazu Energie nötig. Ebenso, wenn man eine Tasche weiter von der Erde entfernt, sie also hochhebt. Wenn man annimmt, dass sich der Magnet und die Tasche dadurch nicht verändert haben, ist es sinnvoll anzunehmen, dass die Energie nun im Feld steckt.
Graphische Darstellung von Feldern
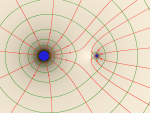
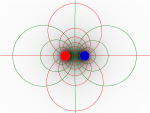
- 1) Drei einfache Beispiele
- Zeichnen Sie einige Feldlinien mit Pfeilen (rot) und Feldflächen (grün) ein.
|
|
|
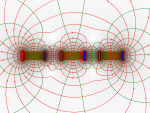
- 2) und noch mehr Felder...
- Zeichnen Sie das Feld folgender Situationen.
- Erklären Sie jeweils mit Hilfe von Druck und Zugspannungen, wie das Feld zieht und drückt.
Feldstärke
- 1) Gravitation auf der Erde und auf anderen Himmelskörpern
- a) Das Gravitationsfeld zieht die Erde und ein Kilogramm Masse mit einer Kraft von ca. 10 Newton aufeinander zu. Die Gravitationsfeldstärke beträgt daher 10 Newton pro Kilogramm: [math]g=\frac{F}{m} = 10\,\rm \frac{N}{kg}[/math]
- b)Ich habe eine Masse von ca. 80kg. Meine Gewichtskraft beträgt daher auf dem Mond:
- [math]F= m\, g = 80\,\rm kg \cdot 1{,}62\,\rm \frac{N}{kg} = 129{,}6\, N[/math]
- c) Die vollständige Tabelle:
Planet
Feldstärke(N/kg)
Masse(kg)
Kraft(N)
Merkur
3,70
80
296
Venus
8,87
75
665
Erde
9,77
12,7
124
Mars
3,69
1000
3690
Jupiter
23
75
1725
- 2) Kraftwirkung im elektrischen Feld
- Die elektrische Feldstärke ist als Ortsfaktor, also als Kraft pro Ladung, definiert:
[math]
\begin{array}{rrcl}
& E & = & \frac{F}{Q} \\
\Rightarrow & F & = & Q\, E = 5\cdot 10^{-9}\,\rm C \cdot 10000\,\rm \frac{N}{C} = 5\cdot 10^{-5}\, N = 0{,}05\, mN
\end{array}
[/math]
- 3) Berechnung der magnetischen Ladung
- Auch die magnetische Feldstärke ist als Ortsfaktor, als Kraft pro magnetische Ladung, definiert:
[math] \begin{array}{rrcl} & H & = & \frac{F}{Q_m} \\ \Rightarrow & Q_m & = & \frac{F}{H} = \frac{0{,}5\,\rm N}{80000\,\rm\frac{N}{Wb}} = 6{,}3 \cdot 10^{-6}\,\rm Wb = 0{,}0063\, mWb \end{array} [/math]
- 4) Definition der Feldstärke
- Die Feldstärke soll eine Aussage über das Feld machen, die unabhängig von der Art des Probekörpers ist. Wegen der Proportionalität zwischen Ladung (Masse) und Kraftwirkung ist die Kraft pro Ladung (Masse) an einer Stelle des Feldes konstant. Dieser Quotient aus Kraft und Ladung (Masse) ist also eine Eigenschaft des Feldes an dieser Stelle.
- Zur Messung der Feldstärke als Kraft pro Ladung muß man die Ladung (oder Masse) und die Kraft messen.
- Ein Coulomb elektrische Ladung ist mit Hilfe von elektrischen Strömen festgelegt worden, als die Ladung, welche in einer Sekunde bei einem Strom der Stärke ein Ampère fließt. Man kann die elektrische Ladung deshalb mit einem Stromstärkemessgerät und einer Uhr messen. (In der Praxis verwendet man einen geeigneten Messverstärker.) Die Masse von einem Kilogramm ist durch das Standardkilogramm in Paris festgelegt und Massen kann man ganz einfach mit einer Waage messen.
- Für die magnetische Ladung gibt es kein übliches Messgerät. Man könnte zwar eines bauen, aber es wäre recht umständlich.[1]
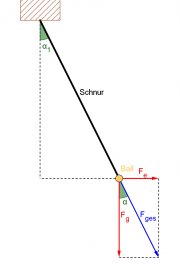
- 5) Tischtennisball im geladenen Kondensator
- Die Summe der elektrischen Kraft und der Gewichtskraft muss genau in Richtung des Fadens ziehen. Daraus folgt:
- [math] \begin{array}{rrcl} & \frac{F_e}{F_g} & = & \tan 4^\circ \\ \Rightarrow & F_e & = & \tan 4^\circ \, m\, g = 0{,}0699 \cdot 0{,}0023\,\rm kg \cdot 10\frac{N}{kg} = 0{,}0699 \cdot 0{,}023\,\rm N = 1{,}6\, mN \end{array} [/math]
Aus der bekannten Feldstärke und der elekrischen Feldkraft kann man nun die Ladung berechnen:
- [math] \begin{array}{rrcl} & E & = &\frac{F_e}{Q} & | \cdot Q \\ \Rightarrow & Q\, E & = & F_e & | \mathopen: E \\ \Rightarrow & Q & = & \frac{F_e}{E}& \\ & & = & \frac{1{,}6\cdot 10^{-3}\,\rm N}{10^{5}\,\rm\frac{N}{C}}& = 16\cdot 10^{-9}\,\rm C = 16\,\rm nC \\ \end{array} [/math]
- 6) Das elektrische Feld der Erde
- Die Summe von elektrischer Kraft und Gewichtskraft muss gerade Null sein, dass heißt die Kräfte sind betragsmäßig gleich groß:
[math]\begin{array}{rrcl} &F_e &=& F_g \\ &Q\, E &=& m\, g \\ \Rightarrow & Q &=& \frac{m\, g}{E} \end{array}[/math]
- Bei wolkenlosen Himmel:
- [math]Q = \frac{1\cdot 10^{-6}\,\rm kg \, 10\rm\frac{N}{kg}}{200\,\rm\frac{N}{C}} = 50\,\rm nC[/math]
- Bei Gewitter:
- [math]Q = \frac{1\cdot 10^{-6}\,\rm kg \, 10\rm\frac{N}{kg}}{30000\,\rm\frac{N}{C}} = 0{,}33\,\rm nC[/math]
Potential
- 1) Potentialunterschiede am Schauinsland
- Der Schauinsland im Schwarzwald hat eine Höhe von 1284 ü NHN, die Stadt Freiburg liegt am Fuße des Schauinslands auf 278 ü NHN.
- a) Wieviel Energie benötigt man, um eine Wasserflasche mit 1kg Masse (einen Rucksack mit 15kg Masse) von Freiburg auf den Schauinsland zu bringen?
- Bei einem Höhenunterschied h berechnet sich die potentielle Energie als
- [math]E_{pot}=m\,g h = 1\,\rm kg \cdot 9{,}81\,{\rm \frac{N}{kg}}\cdot (1284\,\rm m - 278\,\rm m) = 1\,\rm kg \cdot 9{,}81\,{\rm \frac{N}{kg}}\cdot 1006\,\rm m = 9869 \,\rm Nm = 9{,}869 \,\rm kJ[/math]
- Für den Rucksack benötigt man die 15-fache Energiemenge, weil die potentielle Energie proportional zur Masse ist:
- [math]E_{pot}=m\,g h = 15\cdot 9{,}869 \,\rm kJ = 14{,}8 \,\rm kJ[/math]
- b) Wie groß ist die Potentialdifferenz zwischen Freiburg und dem Schauinsland?
- Die Potentialdifferenz gibt den Unterschied der potentiellen Energie pro kg an. Und genau die hat man bereits ausgerechnet, sie beträgt [math]9{,}869 \,\rm{\frac{kJ}{kg}} [/math]
- c) Das Nullniveau der potentiellen Energie soll auf Meereshöhe liegen. Berechne das Potential des Gravitationsfeldes für Freiburg und den Schauinslandgipfel.
- Das Potential gibt die potentielle Energie pro Masse an:
- Potential für Freiburg: [math]\varphi = \frac{E_{pot}}{m} = \frac{m\, g h}{m} = gh = 9{,}81\,{\rm \frac{N}{kg}}\cdot 278\,\rm m = 2727\,{\rm \frac{Nm}{kg}} = 2727\,{\rm \frac{J}{kg}}[/math]
- Potential für den Schauinsland: [math]\varphi = gh = 9{,}81\,{\rm \frac{N}{kg}}\cdot 1284\,\rm m = 12596\,{\rm \frac{Nm}{kg}} = 12596\,{\rm \frac{J}{kg}}[/math]
- d) Zeichne das Gravitationsfeld oberhalb von Freiburg mit Hilfe einiger Feldlinien und den Potentialflächen von 0J/kg, 2000J/kg, 4000J/kg, ... , 14000J/kg.
- 2) Ein Plattenkondensator
- Die beiden Platten eines Kondensators werden an eine Hochspannungsquelle von 10kV angeschlossen. Die Platten sind 20 cm x 20 cm groß und 5cm voneinander entfernt. Der Einfachheit halber gehen wir davon aus, dass sich nur zwischen den Platten ein elektrisches Feld befindet, welches deshalb auch homogen ist.
- a,b,e)
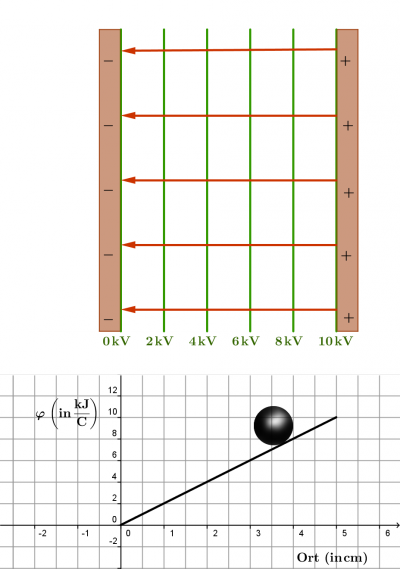
- c) Wie groß ist die Stärke des elektrischen Feldes zwischen den Platten?
- [math]E=\frac{\triangle\varphi}{\triangle s}=\rm \frac{10\, kV}{0{,}05\, m}=200000\frac{V}{m}=200000\frac{N}{C}[/math]
- d) Ein Tischtennisball wird an einem sehr langen Faden in das Feld gehängt. Durch den langen Faden wird der Ball bei einer Auslenkung aus der Ruhelage kaum angehoben. Welche Art von Bewegung vollzieht er, wenn man ihn kurz mit der positiv geladenen Platte in Berührung bringt?
- Der Ball wird immer schneller, er bekommt Energie aus dem Feld. Wegen der konstanten Feldstärke ist auch die beschleunigende Kraft konstant. Der Ball wird gleichmäßig beschleunigt.
- e) Vergleichen Sie die Bewegung mit dem Rollen einer Kugel im Potential.
- Im Modell rollt der Ball die schiefe Potentialebene hinunter. Die potentielle Energie sinkt, die kinetische Energie steigt an.
- f) Wieviel Energie würde ein mit +1C geladener Ball (ein Elektron) erfahren, dass sich von der positiven zur negativen Platte bewegt?
- [math]\varphi=\frac{W}{Q}[/math]
- [math]\Rightarrow W_{\rm Ball} = Q\,\varphi = \rm 1\, C \cdot 10\rm \frac{kJ}{C} = 10\,kJ[/math]
- [math]\Rightarrow W_e = Q\,\varphi = e\,\varphi \quad( = e\cdot 10\,\rm kV = 10\,\rm keV ) = \rm 1{,}6\cdot10^{-19} C \cdot 10\frac{kJ}{C} = 1{,}6\cdot 10^{-15} J[/math]
- g) Wie schnell wäre er (das Elektron) an der negativen (positiven) Platte?
- An der negativen Platte ist die gesamte potentielle Energie in kinetische Energie gewandelt worden:
- [math]W_{\rm kin}=\frac{1}{2}\,m\,v^2[/math]
- [math]\Rightarrow v_{\rm Ball}=\sqrt{\frac{2\, W}{m}}= \sqrt{\frac{2\cdot 10\,\rm kJ}{0,002\,\rm kg}}=3160\rm \frac{m}{s}\approx 11400 \rm \frac{km}{h}[/math]
- Das ist unrealistisch schnell und liegt daran, dass man einen Tischtennisball normalerweise nur mit ca 10nC laden kann!
- [math]\Rightarrow v_e=\sqrt{\frac{2\, W}{m}}= \sqrt{\frac{2\cdot 1{,}6\cdot 10^{-15} \rm J}{9{,}1\cdot 10^{-31}\rm kg}}= 59300000\frac{m}{s}[/math]
- Das Elektron kann in einer Vakuumröhre tatsächlich auf so eine hohe Geschwindigkeit beschleunigt werden! Das sind ca. 20% der Lichtgeschwindigkeit von 300000 km/s.
- 3) Eine Batterie
- Ein geladener Akku hat eine Spannung von 1,2V. Der Akku wird mit einem 2m langem Kabel kurzgeschlossen, wodurch das Kabel erwärmt wird. (Der Einfachheit halber nehmen wir an, dass die Spannung dabei zeitlich konstant ist.)
- a) Jedes Coulomb Ladung erhält 1,2 Joule Energie, das Elektron erhält also die Energiemenge:
- [math]E_{pot}=Q \, \Delta \varphi = Q\, U = 1{,}6 \cdot 10^{-19} \mathrm{C} \cdot 1{,}2\, \rm V = 1{,}92 \cdot 10^{-19} \mathrm{J}[/math]
- b) Die Feldstärke berechnet sich als Potentialänderung pro Strecke:
- [math]E=\frac{\Delta \varphi}{\Delta s} = \frac{1{,}2\,\rm V}{2\,\rm m} = 0{,}6 \, {\rm \frac{V}{m}} = 0{,}6 \, {\rm \frac{N}{C}}[/math]
- c) Die Kraft auf eine Ladung berechnet sich als Ladung mal Ortsfaktor:
- [math]F=Q \, E = 1{,}6 \cdot 10^{-19} \mathrm{C} \cdot 0{,}6 \, {\rm \frac{N}{C}} = 0{,}96 \cdot 10^{-19} \mathrm{N}[/math]
- d) Jedes Coulomb Ladung erhält 1,2 J Energie:
- [math]E_{pot}= Q \, \Delta \varphi = Q\, U = 7200\,\rm C \cdot 1{,}2\,\rm V = 8640\,\rm J[/math]
- (Das entspricht etwa dem Energiegehalt von 0,25ml Benzin.)
- 4) Ein Satellit im Schwerefeld der Erde
- a) Wieviel Energie benötigt man, um den Satellit (Masse 800 kg) an die markierte Stelle zu heben?
- Das Potential steigt ungefähr von -62 MJ/kg auf -16 MJ/kg. Die Potentialdifferenz beträgt daher:
- [math]\Delta \varphi = 46\,\rm \frac{MJ}{kg}[/math]
- Der Zahlenwert gibt an, wieviel Energie man für ein Kilogramm Masse bräuchte. Für den Satelliten braucht man also die Energie:
- [math]E_{pot} = m\,\rm \Delta \varphi = 500\,\rm kg \cdot 46\,\rm\frac{MJ}{kg} = 23000\,\rm MJ[/math]
- (Das entspricht dem Energiegehalt von 800l Benzin!)
- b) Welche Kraft wirkt dort ungefähr auf ihn?
- Die Steigung des Potentials ist die Feldstärke, die man hier näherungsweise mit dem Differenzenquotienten bestimmt. (Man kann das in dieser Animation besser als im Bild ablesen.)
- Das Potential steigt im Abstand von ca. 2,5 Erdradien bis zu 8 Erdradien von ca. -24 MJ/kg auf -8MJ/kg:
- [math]g = \varphi ' \approx \frac{\Delta \varphi}{\Delta s} \approx \frac{-8\,\rm \frac{MJ}{kg} - (-24\,\rm \frac{MJ}{kg})}{8\,r_E-2{,}5\,r_E} = \frac{16\,\rm \frac{MJ}{kg}}{6{,}5\,r_E} = \frac{16\cdot 10^{6}\rm \frac{J}{kg}}{6{,}5\cdot 6370 \cdot 10^{3}\,\rm m} \approx 0{,}39\,\rm \frac{N}{kg} [/math]
- Die Feldstärke beträgt also dort nur noch ein Zwanzigstel der Feldstärke auf der Erde!
- Dementsprechend klein ist auch die "Gewichtskraft" auf den Satelliten:
- [math]F = m\, g = 500\,\rm kg \cdot 0{,}39\,\rm \frac{N}{kg} =190\,\rm N[/math]
- 5) Mondstation
- a) Wieviel Energie benötigt man, damit man 1 Tonne Nachschub-Material auf eine Mondstation bringen kann?
- Um über den "Potentialberg" zu kommen, muß man die maximale Potentialdifferenz von [math]\Delta \varphi \approx 60\,\rm \frac{MJ}{kg}[/math] überwinden. Danach geht es dann wieder ein wenig "bergab".
- Für eine Tonne Nachschub braucht man daher mindestens die Energie:
- [math]E_{pot} = m\,\Delta\,\varphi = 1000\,\rm kg \cdot 60\,\rm \frac{MJ}{kg} = 60.000 \,\rm MJ[/math]
- b) Wieviel potentielle Energie hat das Material dann auf der Mondoberfläche?
- Weil es nach dem "Potentialberg" wieder ein wenig "bergab" ging, beträgt die Potentialdifferenz zur Erde nur ca. [math]\Delta \varphi \approx 58\,\rm \frac{MJ}{kg}[/math], die potentielle Energie beträgt also nur noch:
- [math]E_{pot} = m\,\Delta\,\varphi = 1000\,\rm kg \cdot 58\,\rm \frac{MJ}{kg} = 58.000 \,\rm MJ[/math]
- c) Vergleichen Sie die Energiemengen mit Benzinmengen! (Ein Kilogramm Benzin enthält ca. 43 MJ Energie, ein Liter Benzin ca. 30 MJ.)
- Man braucht also mindestens 2000l oder 1,3t Benzin, um eine Tonne Nachschub auf den Mond zu bringen! (Man benötigt noch wesentlich mehr, denn für den Flug dorthin muss der Nachschub auch Bewegungsenergie bekommen, die man leider nicht mehr zurückgewinnen kann. Außerdem muss auch die gesamte Rakete mit dem Treibstoff hochgehoben und beschleunigt werden.)
- 6) Das Potential der Erde
Anton steht auf der Erde. Bertha befindet sich einen Erdradius oberhalb der Erdoberfläche in einer Raumkapsel. Cecilie ist zwei Erdradien von der Erde entfernt. (usw.)
- a) Berechnen Sie die Potentialunterschiede zwischen A und B, B und C, ...
- b) Berechnen Sie das Potential an den Stellen A, B, C, ...
- 7) Ein geostationärer Satellit
Ein Satellit (Masse 800 kg) soll in eine geostationäre Umlaufbahn, also in eine Höhe von etwa 36.000 km über der Erdoberfläche. Der Bahnradius beträgt dann ungefähr 42.000 km.
- a) Berechnen Sie mit Hilfe einer Gleichung für die Feldstärke oder des Potential die dazu nötige Energiemenge.
- b) Vergleichen Sie die Energiemengen mit Benzinmengen! (Ein Kilogramm Benzin enthält ca. 43 MJ Energie, ein Liter Benzin ca. 30 MJ.)
Schwere, Elektrische und Magnetische Wechselwirkung (Gravitation, Elektrostatik, Magnetostatik)
Versuche beschreiben und erklären mit der Nahwirkungstheorie.
Segnersches Rad, "Wedelgenerator", ...
Ladung als Quellenstärke und der Fluss eines Feldes
Masse der Erde
- Wieviel (schwere) Masse hat die Erde?
Der Feldfluss durch die Erdoberfläche ist genauso groß wie die Erdmasse:
- [math]\frac{1}{4\pi \,G} \ g \, A = m[/math]
Jetzt muss man nur die Fläche zu [math]A= 4 \pi \, r^2[/math] und die Gravitationskonstante einsetzen:
- [math]\frac{1}{4\pi \,6{,}673\;84\; \cdot 10^{-11} \mathrm{\frac{m^3}{kg \cdot s^2}}} \ 9{,}81 \rm \frac{N}{kg} \, 4 \pi \, (\rm 6380000 m)^2 \approx 5{,}987 \cdot 10^{24}\rm kg[/math]
Das ist schon ein recht vernünftiger Wert im Vergleich zu genaueren Messwerten.
Gravitationsfeldstärke im All
- Wie groß ist die Gravitationsfeldstärke in einem Abstand von 6370 km über dem Erdboden?
Mit Erdmasse
In einem Abstand von 6370km über dem Erdboden ist man 12740km vom Ermittelpunkt entfernt. Man betrachtet den Feldfluss durch eine Kugeloberfläche mit diesem Radius. Dazu kann man die Formel für die Quellenstärke umformen:
- [math]g = 4 \pi \, G\, \frac{m}{A} = 4 \pi \cdot 6{,}67 \cdot 10^{-11} \mathrm{\frac{m^3}{kg \cdot s^2}} \cdot \frac{5{,}99 \cdot 10^{24}\rm kg}{4 \pi \, (12740000\,\rm m)^2} \approx 2{,}45 \,\rm \frac{N}{kg}[/math]
Verdopplung der Entfernung
Durch den doppelten Abstand vom Erdmittelpunkt vergößert sich die Kugelfläche auf das Vierfache. Denn der Radius wird quadriert: [math]A=4 \pi \, r^2[/math]
Da der Fluss durch die Fläche aber gleich bleibt muss die Feldstärke auf ein Viertel abnehmen!
- [math]g = \frac{1}{4} \cdot 9{,}81 \,{\rm\frac{N}{kg}} = 2{,}45 \,{\rm \frac{N}{kg}}[/math]
- Welche Kraft wirkt dort auf einen 1000kg schweren Satelliten?
Die Feldstärke ist der Ortsfaktor:
- [math]g=\frac{F}{m} \qquad \Rightarrow \qquad F = m \, g = 1000\, \rm kg \cdot 2{,}45 \frac{N}{kg} = 2450 \, N[/math]
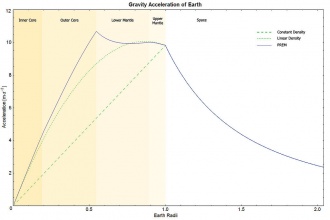
Gravitation in der Erdkugel
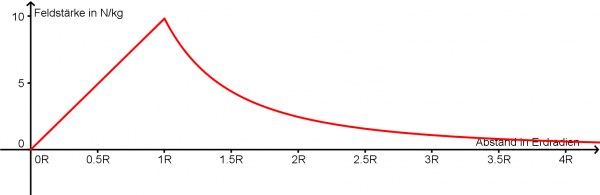
- Wie groß ist die Stärke des Schwerefeldes innerhalb der Erdkugel?
Man betrachtet eine Kugeloberfläche mit dem Radius r. Damit läßt sich die Feldstärke im Abstand r vom Erdmittelpunkt berechnen.
Dazu nehmen wir vereinfachend an, dass die Erde überall die gleiche Massendichte [math]\rho[/math] hat.
Nun ist der Fluss aus der Fläche gleich der enthaltenen Masse. Die Masse außerhalb der Kugel spielt keine Rolle! Das ist erstaunlich. Die Wirkung der Kugelschale außerhalb der Kugel hebt sich gerade auf. (Vgl. Wikipedia: Kugelschale.)
- [math]\frac{1}{4 \pi \, G} \, g \, A = m \qquad \Rightarrow \qquad g = 4 \pi \, G \, \frac{m}{A} = 4 \pi \, G \, \frac{V \, \rho}{A}\qquad .[/math]( mit [math]m= V\, \rho[/math])
Jetzt sieht man, dass es auf das Verhältnis von der enthaltenen Masse, bzw. des Kugelvolumens, zur Oberfläche der Kugel ankommt! Mit [math]A= 4 \, \pi r^2[/math] und [math] V= \frac{4}{3} \, \pi \, r^3[/math] ergibt sich:
- [math]g = 4 \pi \, G \, \frac{\frac{4}{3} \, \pi \, r^3 \, \rho}{4 \, \pi r^2} \qquad \Rightarrow \qquad g = \frac{4}{3}\pi G \rho \ r[/math]
Die Feldstärke ist also proportional zum Abstand des Erdmittelpunktes! Sie nimmt linear zu. Das liegt daran, dass das Volumen in der dritten Potenz zum Radius größer wird, die Oberfläche in der zweiten Potenz.
Probekörper im Kondensator
Zwei geladene Platten, je 30cm x 30cm groß, eine mit 8 10-8 C, die andere mit -8 10-8 C.
- Zur Berechnung der Feldstärke legt man eine Fläche um eine Platte (vgl. hier):
- [math] E= \frac{1}{\epsilon_0} \, \frac{Q}{A} = \frac{1}{8{,}854 \cdot 10^{-12} \frac {\mathrm{A}\,\mathrm{s}} {\mathrm{V}\,\mathrm{m}} } \cdot \frac{8 \cdot 10^{-8}\,\rm C}{0{,}3\,\rm m\cdot 0{,}3\,\rm m} = \frac{1}{8{,}854 \cdot 10^{-12} \frac {\mathrm{A}\,\mathrm{s}} {\mathrm{V}\,\mathrm{m}} } \cdot 8{,}89 \cdot 10^{-7}\,{\rm\frac{C}{m^2}} = 100400\,{\rm \frac{V}{m}} [/math]
- Warum ist dabei die Feldstärke zwischen den Platten nicht vom Abstand der Platten abhängig?
- Wenn man annimmt, dass sich nur zwischen den Platten elektrisches Feld befindet, dann hängt die Feldstärke nur von der Ladungsmenge pro Fläche, der Flächenladungsdichte ab. ( Eine genauere Erklärung steht hier.)
Zwischen die Platten wird ein negativ geladener Tischtennisball gehängt. Auf ihn wirkt eine Kraft von 0,01 N.
- Der Ball wird in Richtung der positiv geladenen Platte gezogen.
- Aus der Feldstärke ergibt sich die Menge der Probeladung:
- [math]E=\frac{F}{Q}\quad \Rightarrow \quad Q=\frac{F}{E} = \frac{0{,}01\,\rm N}{100400\,{\rm \frac{N}{C}}} = 10\cdot 10^{-8}\,\rm C = 100 \,\rm nC[/math]
Fußnoten
- ↑ Siehe auch Die magnetische Feldstärke und Messung der magnetischen Ladung (4st).